37 KiB

Raw Blame History

jupyter

jupytext

kernelspec

formats

text_representation

ipynb,md

extension	format_name	format_version	jupytext_version
.md	markdown	1.2	1.6.0

display_name	language	name
Python 3	python	python3

Ce calepin est composé de deux parties :

la première partie est une rapide présentation du $\lambda$-calcul illustrée par l'utilisation d'un module permettant de définir et transformer des $\lambda$-termes.
la deuxième partie reprend la partie « pouvoir d'expression du $\lambda$-calcul » en l'illustrant avec les lambda-expressions du langage Python.

$\lambda$-calcul

Le $\lambda$-calcul a été introduit dans les années 1930, principalement par Alonzo Church pour des questions de fondements mathématiques, semblables à celles qui ont conduit, à la même époque, Alan Turing à concevoir les machines qui portent son nom maintenant.

Avec les machines de Turing, le $\lambda$-calcul est l'un des principaux outils permettant d'étudier l'informatique théorique. Il est en particulier le fondement de la programmation fonctionnelle, et des langages de programmation comme Lisp, Scheme, ML, Haskell lui doivent beaucoup.

Les $\lambda$-termes

Sommaire de cette partie :

définition des $\lambda$-termes
variables libres, liées. Sous-termes

Le tout illustré avec une classe Python pour représenter et manipuler des $\lambda$-termes.

Définition des $\lambda$-termes

En principe, les $\lambda$-termes sont des mots sur lesquels certaines opérations sont possibles. Ces mots ont vocation à pouvoir exprimer des fonctions, ainsi que leur application à un argument.

Formellement, l'alphabet \Sigma utilisé pour les $\lambda$-termes est constitué :

d'un ensemble infini dénombrable de variables V=\{x, y, z, t, ...\} ;
et d'un ensemble de cinq symboles \mathcal{S}=\{\lambda, ., (, ), ESP\}, ESP désignant l'espace. Ainsi \Sigma = V\cup \mathcal{S}.

Les $\lambda$-termes sont construits inductivement à l'aide des trois règles

toute variable est un $\lambda$-terme ;
si T est un $\lambda$-terme et x une variable, alors \lambda x.T est un $\lambda$-terme, que l'on appelle abstraction de T par x ;
si T et S sont deux $\lambda$-termes, alors (T\ S) est un $\lambda$-terme, que l'on appelle application de T à S.

L'ensemble \Lambda des $\lambda$-termes est donc le plus petit sous-ensemble de \Sigma^* contenant V et stable par abstraction et application.

Une classe pour les $\lambda$-termes

Le module lambda_calcul définit une classe Lambda_terme permettant de construire et manipuler des objets représentant des $\lambda$-termes.

Remarque : ce module fait appel au modulesly qui permet de définir des analyseurs lexicaux et syntaxiques. Ce module doit donc être préalablement installé (pip install sly).

from lambda_calcul import Lambda_terme

Construction de $\lambda$-termes

L'une des façons les plus simples de construire des $\lambda$-termes est d'invoquer le constructeur Lambda_terme avec une chaîne de caractères les représentant.

T1 = Lambda_terme("x")
T2 = Lambda_terme("(x x)")
T3 = Lambda_terme("!x.x")
T4 = Lambda_terme('!x.(x y)')
T5 = Lambda_terme('(!x.(x y) x)')

Les objets de la classe Lambda_terme peuvent être convertis en chaînes de caractères et imprimés.

termes = (T1, T2, T3, T4, T5)
for t in termes:
    print(t)

La syntaxe autorisée pour les $\lambda$-termes est

pour les variables : n'importe quelles chaîne de caractères ne contenant que des lettres (latins) non accentuées majuscules ou minuscules, ainsi que des chiffres. Autrement dit n'importe quelle chaîne correspondant à l'expression régulière [A-Za-z][A-Za-z0-9]*.
pour les abstractions : n'importe quelle chaîne débutant par ! ou \lambda suivie d'une variable, suivie d'un point . suivi d'une chaîne décrivant un $\lambda$-terme. Autrement dit n'importe quelle chaîne satisfaisant (!|λ)VAR.LAMBDA-TERME.
pour les applications : n'importe quelle chaîne débutant par une parenthèse ouvrante ( et terminant par une parenthèse fermante ) et comprenant entre les deux la description de deux $\lambda$-termes séparés par un ou plusieurs espaces. Autrement dit n'importe quelle chaîne satisfaisant (LAMBDA-TERME ESPACES LAMBDA-TERME).

Remarque : le parenthésage des applications est obligatoire, contrairement à la convention d'associativité à gauche qui permet usuellement d'écrire M\ N\ P au lieu de ((M\ N)\ P). De même deux abstractions successives doivent être explicitement écrites : il n'est pas possible d'écrire \lambda xy.(x\ y), il faut écrire \lambda x.\lambda y.(x\ y).

Les passages à la ligne sont autorisés dans la chaîne transmise au constructeur.

print(Lambda_terme('''(james
                   bond007)'''))

L'exception LambdaSyntaxError est déclenchée en cas de présence de caractères non autorisés ou de malformation syntaxique.

# Lambda_terme('bond 007')

# Lambda_terme('(james bond007 !)')

Autres constructions

Deux méthodes permettent de construire de nouveaux $\lambda$-termes à partir de $\lambda$-termes existant.

La méthode abstrait permet de construire une abstraction.

print(T1.abstrait('x'))
print(T2.abstrait('y'))

La méthode applique construit une application d'un terme sur un autre.

print(T2.applique(T3))
print(T3.applique(T2))

Quelques prédicats

Trois prédicats est_variable, est_abstraction et est_application permettent de reconnaître la nature d'un $\lambda$-terme.

# pour rappel des termes définis
for t in termes:
    print(t)

tuple(t.est_variable() for t in termes)

tuple(t.est_abstraction() for t in termes)

tuple(t.est_application() for t in termes)

Variables libres, variables liées

Parmi les variables figurant dans un $\lambda$-terme, certaines sont dites libres, et d'autres liées.

Les variables libres sont celles qui ne sont pas sous la portée d'une abstraction. L'ensemble FV(T) des variables libres d'un $\lambda$-terme T est défini inductivement par les trois règles :

FV(x) = \{x\}.
FV(\lambda x.T) = FV(T)\setminus\{x\}.
FV((T_1\ T_2)) = FV(T_1)\cup FV(T_2).

Les variables liées sont celles qui sont sous la portée d'une abstraction. L'ensemble BV(T) des variables liées d'un $\lambda$-terme T est défini inductivement par les trois règles :

BV(x) = \emptyset.
BV(\lambda x.T) = BV(T)\cup \{x\} si x\in FV(T), sinon BV(\lambda x.T) = BV(T).
BV((T_1\ T_2)) = BV(T_1)\cup BV(T_2).

La méthode variables donne sous un couple constitué de l'ensemble des variables libres et de l'ensemble des variables liées du $\lambda$-terme.

tuple(t.variables() for t in termes)

Remarque : Dans un $\lambda$-terme, une variable peut être à la fois libre et liée comme le montre l'exemple du terme T5 qui contient deux occurrences de la variable x, la première étant liée et la seconde libre. Pour être plus précis, on devrait plutôt parler d'occurrence libre ou liée d'une variable.

Un $\lambda$-terme sans variable libre est appelé terme clos, ou encore combinateur.

Sous-termes

Hormis les variables, les $\lambda$-termes sont construits à partir d'autres $\lambda$-termes qui eux-mêmes peuvent être construits à l'aide d'autres $\lambda$-termes encore.

Un $\lambda$-terme contient donc des sous-termes.

Voici comment l'ensemble ST des sous-termes d'un $\lambda$-terme est défini inductivement selon la structure de ce terme.

Les variables n'ont qu'un seul sous-terme : elles-mêmes. ST(x) = \{x\}.
Les sous-termes d'une abstraction sont, outre l'abstration elle-même, les sous-termes de son corps. ST(\lambda x.T) = \{\lambda x.T\}\cup ST(T).
Les sous-termes d'une application sont, outre l'application elle-même, les sous-termes des deux termes la composant. ST((T_1\ T_2)) = \{(T_1\ T_2)\}\cup ST(T_1)\cup ST(T_2).

La méthode sous_termes donne la liste des sous-termes d'un $\lambda$-terme. L'ordre dans lequel figurent les sous-termes dans cette liste est l'ordre d'apparition de ces sous-termes dans une lecture de gauche à droite (autrement dit, un ordre préfixe).

for t in T5.sous_termes():
    print(t)

$\beta$-réduction ou calculer avec des $\lambda$-termes

Substitution

Étant donnés deux $\lambda$-termes T et R, et une variable x, on note T[x:= R] le $\lambda$-terme obtenu en substituant le terme R à toutes les occurrences libres de la variable x dans le terme T.

Si T est une variable, T[x:=R] = R si T=x et T[x := R] = T si T\neq x.
Si T=(T_1\ T_2) est une application, T[x:=R] = (T_1[x:=R]\ T_2[x := R]).
Si T=\lambda y.S est une abstraction, alors il faut distinguer deux cas pour définir T[x:=R]
- si y\not\in FV(R), alors T[x:=R] = \lambda y.S[x:= R].
- si y\in FV(R), alors T[x:=R] = \lambda z.S[y:=z][x:=R], la variable z étant une nouvelle variable n'apparaissant pas dans S ni dans R. On procède à un renommage de la variable d'abstraction ($y$) pour éviter que les occurrences libres de y de R n'entrent sous la portée de l'abstraction.

La méthode subs renvoie le terme obtenu en substituant un $\lambda$-terme à toutes les occurrences libres d'une variable.

# substitution dans une variable
print('T1 = {:s}'.format(str(T1)))
x = 'y'; R = Lambda_terme('(y x)')
print('T1[{:s}:={:s}] = {:s}'.format(x, str(R), str(T1.subs(x, R))))
x = 'x'
print('T1[{:s}:={:s}] = {:s}'.format(x, str(R), str(T1.subs(x, R))))

# substitution dans une application
print('T2 = {:s}'.format(str(T2)))
x = 'y'; R = Lambda_terme('(y x)')
print('T2[{:s}:={:s}] = {:s}'.format(x, str(R), str(T2.subs(x, R))))
x = 'x'
print('T2[{:s}:={:s}] = {:s}'.format(x, str(R), str(T2.subs(x, R))))

# substitution dans une abstraction
print('T4 = {:s}'.format(str(T4)))
x = 'x'; R = Lambda_terme('(y z)')
print('T4[{:s}:={:s}] = {:s}'.format(x, str(R), str(T4.subs(x, R))))
x = 'y'; R = Lambda_terme('(y z)')
print('T4[{:s}:={:s}] = {:s}'.format(x, str(R), str(T4.subs(x, R))))
x = 'y'; R = Lambda_terme('(y x)')
print('T4[{:s}:={:s}] = {:s}'.format(x, str(R), str(T4.subs(x, R))))

Remarque : on peut utiliser la substitution pour construire des $\lambda$-termes à partir d'autres existants.

print(Lambda_terme('(!z.(T2 T3) T4)').subs('T2', T2).subs('T3', T3).subs('T4', T4))

Réduire un terme

L'idée principale qui motive la notion de réduction est qu'une abstraction \lambda x.T représente une fonction x \mapsto T, et qu'une application d'une abstraction à un terme R, (\lambda x.T\ R) représente l'application de la fonction au terme R.

De la même façon que l'application la fonction x\mapsto x^2+2x -1 à un nombre y se ramène au calcul de l'expression y^2+2y-1 obtenue en substituant y à x, l'application (\lambda x.T\ R) doit se réduire au terme T[x:=R].

Un terme de la forme (\lambda x.T\ R), autrement dit une application d'une abstraction à un terme, est appelé redex.

La réduction d'un redex est une relation, notée \rightarrow_\beta, est définie par

 (\lambda x.T\ R) \rightarrow_\beta T[x:=R].

On peut étendre cette notion de réduction à tout $\lambda$-terme dont l'un au moins de ses sous-termes est un redex. Le terme réduit correspondant étant celui obtenu en remplaçant un sous-terme redex par son réduit.

Selon cette définition, seuls les $\lambda$-termes ayant au moins un redex parmi leurs sous-termes peuvent être réduits. Les $\lambda$-termes ne contenant aucun redex sont dit irréductibles ou encore sont des formes normales.

La méthode est_redex permet de distinguer les $\lambda$-termes qui sont des redex.

for t in termes:
    print(t, t.est_redex())

T6 = T4.applique(T5)
for t in T6.sous_termes():
    print(t, t.est_redex())

La méthode reduit réduit les redex. La valeur de l'expression T.reduit() est un couple (Lambda_terme, bool) dont la valeur dépend du $\lambda$-terme T :

si T contient un redex, alors le booléen a la valeur True et la première composante du couple est le $\lambda$-terme obtenu en remplaçant le redex le plus à gauche dans T par le terme obtenu par une étape de réduction.
si T ne contient aucun redex, alors le couple est (T, False).

t, reduit = T2.reduit()
print(T2)
print(reduit)
print(t)

T7, reduit = T6.reduit()
print(T6)
print(reduit)
print(T7)

Le terme T6 contient deux redex. Comme il a été signalé la méthode reduit réduit le redex le plus à gauche, et dans le cas de T6 le redex le plus à gauche est T6 lui-même. Et cela donne le terme T7.

Mais comme T6 = (T4 T5), et que T5 est un redex, considérons le terme (T4 T5') dans lequel T5' est le terme obtenu en réduisant le redex T5.

T5bis, reduit = T5.reduit()
T7bis = T4.applique(T5bis)
print(T5)
print
print(T7bis)

Nous voyons donc qu'un $\lambda$-terme peut se réduire de plusieurs façons (en fait d'autant de façon que le terme contient de sous-termes qui sont des redex).

En particulier nous avons

T6 \rightarrow_\beta T7 et
T6 \rightarrow_\beta T7bis.

Si nous envisageons les \beta reductions comme des étapes de calcul, nous avons donc deux voies distinctes pour « calculer » T6.

Poursuivons le calcul pour chacun des deux termes T7 et T7bis qui ne sont pas des formes normales.

T8, _ = T7.reduit()
T8bis, _ = T7bis.reduit()
print('{} = {} : {}'.format(str(T8), str(T8bis), T8==T8bis))

Après une nouvelle étape de réduction nous obtenons le même terme ((x\ y)\ y) qui est irréductible. On peut dire que par deux calculs différents T6 se calcule, ou se normalise, en ((x\ y)\ y). On écrit

 \mathtt{T6} \twoheadrightarrow_{\beta} ((x\ y)\ y),

la notation T\twoheadrightarrow_{\beta} R signifiant qu'il y a un nombre quelconque (y compris nul) d'étapes de $\beta$-réduction pour arriver au terme R en partant de T (dit en terme plus savant, la relation \twoheadrightarrow_\beta est la clôture réflexive et transitive de la relation $\rightarrow_\beta$).

Formes normales, normalisation

On dit d'un $\lambda$-terme T qu'il est normalisable s'il existe un $\lambda$-terme R irréductible tel que

 T\twoheadrightarrow_{\beta} R.

Dans ce cas, on dit que R est une forme normale de T.

Par exemple, T6 est normalisable et admet ((x\ y)\ y) pour forme normale.

Deux questions se posent naturellement :

est-ce que tout $\lambda$-terme est normalisable ?
un $\lambda$-terme normalisable peut-il avoir plusieurs formes normales ?

La réponse à la première question est négative. Il suffit pour s'en convaincre de considérer le terme

\Omega = (\lambda x.(x\ x)\ \lambda x.(x\ x)),

qui est un redex et est donc réductible.

OMEGA = Lambda_terme('(!x.(x x) !x.(x x))')
print(OMEGA)
t, reduit = OMEGA.reduit()
print(reduit)
print('{} -> {}'.format(str(OMEGA), str(t)))
print(t==OMEGA)

Le terme \Omega n'a qu'un seul redex. Il n'y a donc qu'une seule façon de le réduire et cette réduction donne le terme \Omega lui-même. Quelque soit le nombre d'étapes de réduction qu'on effectue on garde toujours le même terme : \Omega n'est donc pas normalisable.

Il existe donc des termes non normalisables, et \Omega en est un exemple les plus simples.

Venons-en maintenant à la deuxième question : un terme normalisable peut-il avoir plusieurs formes normales ?

Cette question est naturelle puisque lorsqu'un $\lambda$-terme possède plusieurs redex, il y a plusieurs façons de le réduire, et il se pourrait bien que ces voies différentes mènent à des formes normales différentes.

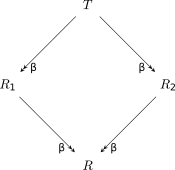
Cela n'a pas été le cas pour le terme T6. Et il se trouve que cet exemple particulier reflète la situation générale, car la relation de $\beta$-réduction satisfait une propriété qu'on appelle propriété du diamant.

Propriété du diamant Soit T un $\lambda$-terme qui peut se réduire en un nombre fini d'étapes en deux termes différents R_1 et R_2. Alors il existe un terme R en lequel chacun des deux termes R_1 et R_2 se réduit en un nombre quelconque (y compris nul) d'étapes.

Cette propriété doit son nom à la figure qui l'illustre. Cette propriété est aussi connue sous le nom de confluence de la $\beta$-réduction.

Conséquence de la propriété du diamant : Un $\lambda$-terme normalisable ne peut avoir qu'une seule forme normale.

Maintenant que nous avons répondu aux deux questions que nous nous sommes posées, il en vient une troisième.

Étant donné que certains $\lambda$-termes sont normalisables et d'autres non, y a-t-il un moyen de les reconnaître ?

Si par moyen nous entendons un algorithme général prenant un $\lambda$-terme en entrée, et répondant OUI si ce terme est normalisable et NON dans le cas contraire, alors la réponse est non. Aucun algorithme ne permet de distinguer les termes normalisables de ceux qui ne le sont pas. Le problème de la reconnaissance des termes normalisables est indécidable.

Dit en d'autres termes, l'ensemble des termes normalisables n'est pas récursif. En revanche il est récursivement énumérable. En effet, si un terme est normalisable, pour s'en rendre compte il suffit de suivre tous les chemins de réduction. L'un d'eux mène à un terme irréductible et on le trouvera en un nombre fini d'étapes.

La méthode forme_normale calcule la forme normale d'un terme normalisable si ce terme l'est, et ne renvoie rien dans le cas contraire.

print(T6.forme_normale())

print(OMEGA.forme_normale())

Hmmmm ... Comment est-ce possible puisque nous venons de voir qu'aucun algorithme ne permet de décider si un terme est normalisable ?

En fait le nombre d'étapes de réduction dans le calcul d'une forme normale est limité (par défaut à 100 étapes maximum). On peut visualiser chaque étape de calcul avec le paramètre optionnel verbose auquel il faut attribuer la valeur True.

T6.forme_normale(verbose=True)

On voit que la forme normale du terme T6 est calculé en trois étapes.

Pour un terme non normalisable les calculs peuvent (en principe) être infinis. Voici la tentative de détermination d'une forme normale pour le terme \Omega limité à dix étapes à l'aide du paramètre optionnel nb_etapes_max.

OMEGA.forme_normale(verbose=True, nb_etapes_max=10)

$\beta$-équivalence

La relation \twoheadrightarrow_\beta n'est pas symétrique. En effet, en général, si T\twoheadrightarrow_\beta R, on n'a pas R\twoheadrightarrow_\beta T.

En considèrant que la forme normale d'un terme normalisable représente sa « valeur », on peut définir une relation d'équivalence sur les $\lambda$-termes normalisables. Cette relation d'équivalence est la clôture symétrique de la relation de réduction \twoheadrightarrow_\beta.

Deux $\lambda$-termes T et S (normalisables ou non) sont dit $\beta$-équivalents, et on note T=_\beta S, s'il existe un terme R tel que T\twoheadrightarrow_\beta R et S\twoheadrightarrow_\beta R.

Ainsi deux termes normalisables ayant la même forme normale sont $\beta$-équivalents.

Théorème du point fixe Pour tout $\lambda$-terme T, il existe un $\lambda$-terme X tel que

 (T\ X) =_\beta X.

La démonstration de ce théorème se fait en considérant les $\lambda$-termes

 W = \lambda x.(T\ (x\ x)),

 X = (W\ W).

Il est clair que

 X \rightarrow_\beta (T\ (W\ W)) = (T\ X),

et donc que

 X =_\beta (T\ X).

W = Lambda_terme('!x.(T (x x))')
X = W.applique(W)
print(X)
print(X.reduit()[0])

Remarque À noter que dans la démonstration du théorème du point fixe, pour établir que (T\ X) =_\beta X, on a montré que X se réduit en (T\ X) et non le contraire.

Pouvoir d'expression du $\lambda$-calcul

Dans cette section, nous allons découvrir que le $\lambda$-calcul permet

de représenter les nombres entiers et de définir les opérations arithmétiques de base
de définir des couples, listes, structures à la base de nombreuses autres structures de données
de définir des booléens, et de simuler des expressions conditionnelles
d'itérer des fonctions,
d'exprimer n'importe quelle fonction récursive.

Bref, d'un certain point de vue le $\lambda$-calcul est un langage de programmation ... certes assez peu efficace comme on pourra s'en rendre compte.

Booléens, opérateurs logiques et conditionnelles

Les deux booléens VRAI et FAUX

On peut représenter les deux booléens VRAI et FAUX par les $\lambda$-termes

 VRAI = \lambda x.\lambda y.x,

 FAUX = \lambda x.\lambda y.y.

VRAI = Lambda_terme('!x.!y.x')
FAUX = Lambda_terme('!x.!y.y')

Le terme IF

Ce choix peut être justifiée a posteriori en considérant que l'expression conditionnelle fréquente en programmation

  IF c THEN a ELSE s

peut être facilement simulée à l'aide d'abstractions des variables c, a et s par le $\lambda$-terme

 \mathtt{IF} = \lambda c.\lambda a.\lambda s.((c\ a)\ s).

IF = Lambda_terme('!c.!a.!s.((c a) s)')

IF.applique(VRAI).applique(Lambda_terme('ALORS')).applique(Lambda_terme('SINON')).forme_normale(verbose=True)

IF.applique(FAUX).applique(Lambda_terme('ALORS')).applique(Lambda_terme('SINON')).forme_normale(verbose=True)

Remarque Le $\lambda$-terme \mathtt{IF} permet d'exprimer des $\lambda$-termes ayant une forme normale bien que l'une ou l'autre de ses sous-termes n'en aient pas, comme par exemple

(((\mathtt{IF}\, \mathtt{VRAI})\, \mathtt{ALORS})\, \mathtt{OMEGA}) qui se réduit en \mathtt{ALORS} (et a donc une forme normale si \mathtt{ALORS} en a une) bien que \mathtt{OMEGA} n'en ait pas ;
ou (((\mathtt{IF}\, \mathtt{FAUX})\, \mathtt{OMEGA})\, \mathtt{SINON}) qui se réduit en \mathtt{SINON}.

Cette propriété est bien utile en programmation, et servira pour la programmation de fonctions récursives.

IF.applique(VRAI).applique(Lambda_terme('ALORS')).applique(OMEGA).forme_normale(verbose=True)

IF.applique(FAUX).applique(OMEGA).applique(Lambda_terme('SINON')).forme_normale(verbose=True)

Le fait que le terme IF se comporte bien comme on l'attend résulte du choix de la stratégie de réduction des redex les plus à gauche en priorité. Si la stratégie choisie avait été de réduire le redex le plus à droite, la réduction de chacun des deux termes précédents aurait conduit à la tentative de réduire le terme \Omega qui échoue puisque celui-ci n'est pas normalisable comme on l'a vu.

Il est facile de définir les opérateurs logiques de base : conjonction, disjonction et négation.

Opérateur ET

L'opérateur logique de conjonction peut être défini par

 ET = \lambda a.\lambda b.(((IF\ a)\ b)\ FAUX).

ET = IF.applique(Lambda_terme('a')).applique(Lambda_terme('b')).applique(FAUX).abstrait('b').abstrait('a')

print(ET)

Et on peut verifier que ce terme satisfait bien à la table de vérité de l'opérateur de conjonction.

ET.applique(VRAI).applique(VRAI).forme_normale(verbose=True) == VRAI

ET.applique(VRAI).applique(FAUX).forme_normale(verbose=True) == FAUX

ET.applique(FAUX).applique(VRAI).forme_normale(verbose=True) == FAUX

ET.applique(FAUX).applique(FAUX).forme_normale(verbose=True) == FAUX

Opérateur OU

L'opérateur logique de disjonction peut être défini par

 OU = \lambda a.\lambda b.(((IF\ a)\ VRAI)\ b).

OU = IF.applique(Lambda_terme('a')).applique(VRAI).applique(Lambda_terme('b')).abstrait('b').abstrait('a')

print(OU)

Et on peut verifier que ce terme satisfait bien à la table de vérité de l'opérateur de disjonction.

OU.applique(VRAI).applique(VRAI).forme_normale(verbose=True) == VRAI

OU.applique(VRAI).applique(FAUX).forme_normale(verbose=True) == VRAI

OU.applique(FAUX).applique(VRAI).forme_normale(verbose=True) == VRAI

OU.applique(FAUX).applique(FAUX).forme_normale(verbose=True) == FAUX

Opérateur NON

L'opérateur de négation peut être défini par le terme

 NON = \lambda a.(((IF\ a)\ FAUX)\ VRAI).

NON = IF.applique(Lambda_terme('a')).applique(FAUX).applique(VRAI).abstrait('a')

print(NON)

NON.applique(VRAI).forme_normale(verbose=True) == FAUX

NON.applique(FAUX).forme_normale(verbose=True) == VRAI

Entiers, successeurs, addition, multiplication et exponentiation

Numéraux de Church

Il existe plusieurs façons de représenter les entiers naturels par un $\lambda$-terme. La représentation donnée ici est connue sous le nom de numéraux de Church.

ZERO = Lambda_terme('!f.!x.x')

UN = Lambda_terme('!f.!x.(f x)')

DEUX = Lambda_terme('!f.!x.(f (f x))')

Successeur

SUC = Lambda_terme('!n.!f.!x.(f ((n f) x))')

TROIS = SUC.applique(DEUX).forme_normale(verbose=True)

TROIS.applique(SUC).applique(ZERO).forme_normale(verbose=True)

Addition

ADD = Lambda_terme('!n.!m.!f.!x.((n f) ((m f) x))')

QUATRE = ADD.applique(UN).applique(TROIS).forme_normale(verbose=True)

CINQ = ADD.applique(TROIS).applique(DEUX).forme_normale(verbose=True)

SEPT = ADD.applique(QUATRE).applique(TROIS).forme_normale(verbose=True)

Multiplication

MUL = Lambda_terme('!n.!m.!f.(n (m f))')

SIX = MUL.applique(DEUX).applique(TROIS).forme_normale(verbose=True)

Exponentiation

EXP = Lambda_terme('!n.!m.(m n)')

HUIT = EXP.applique(DEUX).applique(TROIS).forme_normale(verbose=True)

HUIT == MUL.applique(DEUX).applique(QUATRE).forme_normale()

NEUF = EXP.applique(TROIS).applique(DEUX).forme_normale(verbose=True)

NEUF == ADD.applique(SEPT).applique(DEUX).forme_normale()

Nullité

NUL = Lambda_terme('!n.((n !x.FAUX) VRAI)').subs('FAUX', FAUX).subs('VRAI', VRAI)

print(NUL)

NUL.applique(ZERO).forme_normale(verbose=True) == VRAI

NUL.applique(TROIS).forme_normale(verbose=True) == FAUX

Couples et listes

CONS = Lambda_terme('!x.!y.!s.(((IF s) x) y)').subs('IF', IF)

print(CONS)

UN_DEUX = CONS.applique(UN).applique(DEUX).forme_normale(verbose=True)

CAR = Lambda_terme('!c.(c VRAI)').subs('VRAI', VRAI)

print(CAR)

CAR.applique(UN_DEUX).forme_normale(verbose=True) == UN

CDR = Lambda_terme('!c.(c FAUX)').subs('FAUX', FAUX)

print(CDR)

CDR.applique(UN_DEUX).forme_normale(verbose=True) == DEUX

M = Lambda_terme('M')
CPLE_M = CONS.applique(CAR.applique(M)).applique(CDR.applique(M))

CDR.applique(CPLE_M).forme_normale(verbose=True)

M_PRED = Lambda_terme('!n.(CAR ((n !c.((CONS (CDR c)) (SUC (CDR c)))) ((CONS ZERO) ZERO)))')
print(M_PRED)
PRED = M_PRED.subs('CAR', CAR).subs('CONS', CONS).subs('CDR', CDR).subs('SUC', SUC).subs('ZERO', ZERO)
print(PRED)

PRED.applique(DEUX).forme_normale(verbose=True) == UN

PRED.applique(ZERO).forme_normale(verbose=True) == ZERO

M_SUB = Lambda_terme('!n.!m.((m PRED) n)')
print(M_SUB)
SUB = M_SUB.subs('PRED', PRED)
print(SUB)

SUB.applique(TROIS).applique(UN).forme_normale(verbose=True) == DEUX

M_INF = Lambda_terme('!n.!m.(NUL ((SUB n) m))')
print(M_INF)
INF = M_INF.subs('NUL', NUL).subs('SUB', SUB)

INF.applique(TROIS).applique(UN).forme_normale() == FAUX

INF.applique(UN).applique(TROIS).forme_normale() == VRAI

INF.applique(UN).applique(UN).forme_normale() == VRAI

M_EGAL = Lambda_terme('!n.!m.((ET ((INF n) m)) ((INF m) n))')
print(M_EGAL)
EGAL = M_EGAL.subs('ET', ET).subs('INF', INF)
print(EGAL)

EGAL.applique(UN).applique(UN).forme_normale() == VRAI

EGAL.applique(UN).applique(DEUX).forme_normale() == FAUX

Itération

M_FACTv1 = Lambda_terme('!n.(CDR ((n !c.((CONS (SUC (CAR c))) ((MUL (SUC (CAR c))) (CDR c)))) ((CONS ZERO) UN)))')
print(M_FACTv1)
FACTv1 = M_FACTv1.subs('CONS', CONS).subs('CAR', CAR).subs('CDR', CDR).subs('SUC', SUC).subs('MUL', MUL).subs('UN', UN).subs('ZERO', ZERO)
print(FACTv1)

FACTv1.applique(ZERO).forme_normale() == UN

FACTv1.applique(UN).forme_normale() == UN

print(FACTv1.applique(DEUX).forme_normale())

FACTv1.applique(DEUX).forme_normale(nb_etapes_max=118) == DEUX

FACTv1.applique(TROIS).forme_normale(nb_etapes_max=403) == SIX

FACTv1.applique(QUATRE).forme_normale(nb_etapes_max=1672) == MUL.applique(QUATRE).applique(SIX).forme_normale()

Et la récursivité ?

M_PHI_FACT = Lambda_terme('!f.!n.(((IF ((EGAL n) ZERO)) UN) ((MUL n) (f (PRED n))))')
print(M_PHI_FACT)
PHI_FACT = M_PHI_FACT.subs('IF', IF).subs('EGAL', EGAL).subs('ZERO', ZERO).subs('UN', UN).subs('MUL', MUL).subs('PRED', PRED)
print(PHI_FACT)

BOTTOM = Lambda_terme('!y.OMEGA').subs('OMEGA', OMEGA)
print(BOTTOM)

FACT0 = PHI_FACT.applique(BOTTOM)

FACT0.applique(ZERO).forme_normale() == UN

FACT0.applique(UN).forme_normale(verbose=True, nb_etapes_max=20)

FACT1 = PHI_FACT.applique(FACT0)

FACT1.applique(ZERO).forme_normale() == UN

FACT1.applique(UN).forme_normale(nb_etapes_max=110) == UN

FIX_CURRY = Lambda_terme('!f.(!x.(f (x x)) !x.(f (x x)))')
print(FIX_CURRY)

FACTv2 = FIX_CURRY.applique(PHI_FACT)

FACTv2.applique(ZERO).forme_normale() == UN

FACTv2.applique(UN).forme_normale(nb_etapes_max=113) == UN

FACTv2.applique(DEUX).forme_normale(nb_etapes_max=516) == DEUX

FACTv2.applique(TROIS).forme_normale(nb_etapes_max=2882) == SIX

FACTv2.applique(QUATRE).forme_normale(nb_etapes_max=18668) == MUL.applique(QUATRE).applique(SIX).forme_normale()

PF = FIX_CURRY.applique(Lambda_terme('M'))

PF.forme_normale(verbose=True, nb_etapes_max=10)

FIX_TURING = Lambda_terme('(!x.!y.(y ((x x) y)) !x.!y.(y ((x x) y)))')
print(FIX_TURING)

FACTv3 = FIX_TURING.applique(PHI_FACT)

FACTv3.applique(ZERO).forme_normale() == UN

FACTv3.applique(UN).forme_normale(nb_etapes_max=114) == UN

FACTv3.applique(DEUX).forme_normale(nb_etapes_max=520) == DEUX

FACTv3.applique(TROIS).forme_normale(nb_etapes_max=2897) == SIX

FACTv3.applique(QUATRE).forme_normale(nb_etapes_max=18732) == MUL.applique(QUATRE).applique(SIX).forme_normale()

$\lambda$-calcul avec les lambda-expressions de Python

Dans cette partie, les lambda-expressions de Python vont être utilisées pour représenter les abstractions, et les applications seront des appels de fonction.

Les seuls mots du langage Python que nous utiliserons seront lambda et if. Les autres mots (def, while, for ...) seront bannis. Nous utiliserons aussi les entiers prédéfinis dans le langage avec certaines opérations arithmétiques.

Les booléens

vrai = lambda x: lambda y: x
faux = lambda x: lambda y: y

def booleen_en_bool(b):
    return b(True)(False)

tuple(booleen_en_bool(b) for b in (vrai, faux))

If = lambda c: lambda a: lambda s: c(a)(s)

If(vrai)(1)(2)

If(faux)(1)(2)

#If(vrai)(1)(1/0)

non = lambda b: If(b)(faux)(vrai)

tuple(booleen_en_bool(non(b)) for b in (vrai, faux))

et = lambda b1: lambda b2: If(b1)(b2)(faux)

tuple(booleen_en_bool(et(b1)(b2)) for b1 in (vrai, faux) 
      for b2 in (vrai, faux))

ou = lambda b1: lambda b2: If(b1)(vrai)(b2)

tuple(booleen_en_bool(ou(b1)(b2)) for b1 in (vrai, faux) 
      for b2 in (vrai, faux))

Les entiers de Church

zero = lambda f: lambda x: x

un = lambda f: lambda x: f(x)

deux = lambda f: lambda x: f(f(x))

trois = lambda f: lambda x: f(f(f(x)))

def entier_church_en_int(ec):
    return ec(lambda n: n+1)(0)

tuple(entier_church_en_int(n) for n in (zero, un, deux, trois))

suc = lambda n: lambda f: lambda x: f(n(f)(x))

tuple(entier_church_en_int(suc(n)) for n in (zero, un, deux, trois))

def int_en_entier_church(n):
    if n == 0:
        return zero
    else:
        return suc(int_en_entier_church(n - 1))

tuple(entier_church_en_int(int_en_entier_church(n)) for n in range(10))

add = lambda n: lambda m: lambda f: lambda x: n(f)(m(f)(x))

cinq = add(deux)(trois)
entier_church_en_int(cinq)

mul = lambda n: lambda m: lambda f: n(m(f))

six = mul(deux)(trois)
entier_church_en_int(six)

exp = lambda n: lambda m: m(n)

huit = exp(deux)(trois)
entier_church_en_int(huit)

neuf = exp(trois)(deux)
entier_church_en_int(neuf)

est_nul = lambda n : n(lambda x: faux)(vrai)

tuple(booleen_en_bool(est_nul(n)) 
      for n in (zero, un, deux, trois, cinq, six, huit))

Les couples

cons = lambda x: lambda y: lambda z: z(x)(y)

un_deux = cons(un)(deux)

car = lambda c: c(vrai)
cdr = lambda c: c(faux)

entier_church_en_int(car(un_deux)), entier_church_en_int(cdr(un_deux))

pred = lambda n: car(n(lambda c: cons(cdr(c))(suc(cdr(c))))(cons(zero)(zero)))

tuple(entier_church_en_int(pred(int_en_entier_church(n))) for n in range(10))

sub = lambda n: lambda m: m(pred)(n)

entier_church_en_int(sub(huit)(trois))

est_inf_ou_egal = lambda n: lambda m: est_nul(sub(m)(n))

tuple(booleen_en_bool(est_inf_ou_egal(cinq)(int_en_entier_church(n))) 
      for n in range(10))

est_egal = lambda n: lambda m: et(est_inf_ou_egal(n)(m))(est_inf_ou_egal(m)(n))

tuple(booleen_en_bool(est_egal(cinq)(int_en_entier_church(n))) 
      for n in range(10))

Itération

fact = lambda n: cdr(n(lambda c: (cons(suc(car(c)))(mul(suc(car(c)))(cdr(c)))))(cons(zero)(un)))

tuple(entier_church_en_int(fact(int_en_entier_church(n))) for n in range(7))

Combinateur de point fixe

phi_fact = lambda f: lambda n: 1 if n == 0 else n*f(n-1)

bottom = lambda x: (lambda y: y(y))(lambda y:y(y))

f0 = phi_fact(bottom)
f1 = phi_fact(f0)
f2 = phi_fact(f1)
f3 = phi_fact(f2)
f4 = phi_fact(f3)

tuple(f4(n) for n in range(4))

def fact_rec(n):
    if n == 0:
        return 1
    else:
        return n * fact_rec(n - 1)

fact2 = phi_fact(fact_rec)

tuple(fact2(n) for n in range(7))

fix_curry = lambda f: (lambda x: lambda y: f(x(x))(y))(lambda x: lambda y: f(x(x))(y))

fact3 = fix_curry(phi_fact)

tuple(fact3(n) for n in range(7))

Un programme obscur

print((lambda x: (lambda y: lambda z: x(y(y))(z))(lambda y: lambda z: x(y(y))(z))) 
      (lambda x: lambda y: '' if y == [] else chr(y[0])+x(y[1:]))
      (((lambda x: (lambda y: lambda z: x(y(y))(z)) (lambda y: lambda z: x(y(y))(z)))
        (lambda x: lambda y: lambda z: [] if z == [] else [y(z[0])]+x(y)(z[1:])))      
       (lambda x: (lambda x: (lambda y: lambda z: x(y(y))(z))(lambda y: lambda z: x(y(y))(z)))
        (lambda x: lambda y: lambda z: lambda t: 1 if t == 0 else (lambda x: ((lambda u: 1 if u == 0 else z)(t % 2)) * x * x % y)
         (x(y)(z)(t // 2)))(989)(x)(761))
       ([377, 900, 27, 27, 182, 647, 163, 182, 390, 27, 726, 937])))

phiListEnChaine = lambda x: lambda y: '' if y == [] else chr(y[0]) + x(y[1:])

fix_curry(phiListEnChaine)([65+k for k in range(26)])

phiMap = lambda x: lambda y: lambda z: [] if z == [] else [y(z[0])] + x(y)(z[1:])

fix_curry(phiMap)(lambda x: x*x)([1, 2, 3, 4])

phiExpoMod = lambda x: lambda y: lambda z: lambda t: 1 if z == 0 else (lambda u: 1 if u == 0 else y)(z % 2) * x(y)(z//2)(t) ** 2 % t

fix_curry(phiExpoMod)(2)(10)(1000)

37 KiB Raw Blame History

$\lambda$-calcul

Les $\lambda$-termes

Définition des $\lambda$-termes

Une classe pour les $\lambda$-termes

Construction de $\lambda$-termes

Autres constructions

Quelques prédicats

Variables libres, variables liées

Sous-termes

$\beta$-réduction ou calculer avec des $\lambda$-termes

Substitution

Réduire un terme

Formes normales, normalisation

$\beta$-équivalence

Pouvoir d'expression du $\lambda$-calcul

Booléens, opérateurs logiques et conditionnelles

Les deux booléens VRAI et FAUX

Le terme IF

Opérateur ET

Opérateur OU

Opérateur NON

Entiers, successeurs, addition, multiplication et exponentiation

Numéraux de Church

Successeur

Addition

Multiplication

Exponentiation

Nullité

Couples et listes

Itération

Et la récursivité ?

$\lambda$-calcul avec les lambda-expressions de Python

Les booléens

Les entiers de Church

Les couples

Itération

Combinateur de point fixe

Un programme obscur

37 KiB

Raw Blame History