66 KiB

Raw Blame History

jupyter

jupytext

kernelspec

formats

text_representation

ipynb,md

extension	format_name	format_version	jupytext_version
.md	markdown	1.2	1.6.0

display_name	language	name
Python 3	python	python3

Ce calepin est composé de deux parties :

la première partie est une rapide présentation du $\lambda$-calcul illustrée par l'utilisation d'un module permettant de définir et transformer des $\lambda$-termes.
la deuxième partie reprend la partie « pouvoir d'expression du $\lambda$-calcul » en l'illustrant avec les lambda-expressions du langage Python. (CETTE PARTIE RESTE ENCORE A REDIGER)

$\lambda$-calcul

Le $\lambda$-calcul a été introduit dans les années 1930, principalement par Alonzo Church pour des questions de fondements mathématiques, semblables à celles qui ont conduit, à la même époque, Alan Turing à concevoir les machines qui portent son nom maintenant.

Avec les machines de Turing, le $\lambda$-calcul est l'un des principaux outils permettant d'étudier l'informatique théorique. Il est en particulier le fondement de la programmation fonctionnelle, et des langages de programmation comme Lisp, Scheme, ML, Haskell lui doivent beaucoup.

Les $\lambda$-termes

Sommaire de cette partie :

définition des $\lambda$-termes
variables libres, liées. Sous-termes

Le tout illustré avec une classe Python pour représenter et manipuler des $\lambda$-termes.

Définition des $\lambda$-termes

En principe, les $\lambda$-termes sont des mots sur lesquels certaines opérations sont possibles. Ces mots ont vocation à pouvoir exprimer des fonctions, ainsi que leur application à un argument.

En $\lambda$-calcul tout est fonction !

Si f est un $\lambda$-terme, on doit pouvoir l'appliquer à un autre terme x, mais au lieu d'écrire f(x) comme c'est l'usage en mathématiques, on écrit plutôt (f\ x) et cela forme un nouveau terme nommé application.

Il n'y a pas de fonctions à plusieurs variables : toutes les fonctions ont une et une seule variable. Donc si on a en tête de vouloir représenter une fonction à deux variables f(x,y), elle le sera par une fonction à une variable telle que f(x) soit elle aussi une fonction à une variable, et au lieu d'écrire f(x,y) ou même f(x)(y), on écrira ((f\ x)\ y).

Enfin si x est une variable et M un terme dépendant éventuellement de x, on doit pouvoir définir la fonction x\mapsto M. Cette construction est nommée abstraction en $\lambda$-calcul et elle est notée \lambda x.M.

Formellement, l'alphabet \Sigma utilisé pour les $\lambda$-termes est constitué :

d'un ensemble infini dénombrable de variables V=\{x, y, z, t, ...\} ;
et d'un ensemble de cinq symboles \mathcal{S}=\{\lambda, ., (, ), ESP\}, ESP désignant l'espace. Ainsi \Sigma = V\cup \mathcal{S}.

Les $\lambda$-termes sont construits inductivement à l'aide des trois règles

toute variable est un $\lambda$-terme ;
si T est un $\lambda$-terme et x une variable, alors \lambda x.T est un $\lambda$-terme, que l'on appelle abstraction de T par x ;
si T et S sont deux $\lambda$-termes, alors (T\ S) est un $\lambda$-terme, que l'on appelle application de T à S.

L'ensemble \Lambda des $\lambda$-termes est donc le plus petit sous-ensemble de \Sigma^* contenant V et stable par abstraction et application.

Une classe pour les $\lambda$-termes

Le module lambda_calcul définit une classe Lambda_terme permettant de construire et manipuler des objets représentant des $\lambda$-termes.

Remarque : ce module fait appel au modulesly qui permet de définir des analyseurs lexicaux et syntaxiques. Ce module doit donc être préalablement installé (pip install sly).

from lambda_calcul import Lambda_terme

Construction de $\lambda$-termes

L'une des façons les plus simples de construire des $\lambda$-termes est d'invoquer le constructeur Lambda_terme avec une chaîne de caractères les représentant.

T1 = Lambda_terme("x")
T2 = Lambda_terme("(x x)")
T3 = Lambda_terme("!x.x")
T4 = Lambda_terme('!x.(x y)')
T5 = Lambda_terme('(!x.(x y) x)')

Les objets de la classe Lambda_terme peuvent être convertis en chaînes de caractères et imprimés.

termes = (T1, T2, T3, T4, T5)
for t in termes:
    print(t)

La syntaxe autorisée pour les $\lambda$-termes est

pour les variables : n'importe quelles chaîne de caractères ne contenant que des lettres (latins) non accentuées majuscules ou minuscules, ainsi que des chiffres. Autrement dit n'importe quelle chaîne correspondant à l'expression régulière [A-Za-z][A-Za-z0-9]*.
pour les abstractions : n'importe quelle chaîne débutant par ! ou \lambda suivie d'une variable, suivie d'un point . suivi d'une chaîne décrivant un $\lambda$-terme. Autrement dit n'importe quelle chaîne satisfaisant (!|λ)VAR.LAMBDA-TERME.
pour les applications : n'importe quelle chaîne débutant par une parenthèse ouvrante ( et terminant par une parenthèse fermante ) et comprenant entre les deux la description de deux $\lambda$-termes séparés par un ou plusieurs espaces. Autrement dit n'importe quelle chaîne satisfaisant (LAMBDA-TERME ESPACES LAMBDA-TERME).

Remarque : le parenthésage des applications est obligatoire, contrairement à la convention d'associativité à gauche qui permet usuellement d'écrire M\ N\ P au lieu de ((M\ N)\ P). De même deux abstractions successives doivent être explicitement écrites : il n'est pas possible d'écrire \lambda xy.(x\ y), il faut écrire \lambda x.\lambda y.(x\ y).

Les passages à la ligne sont autorisés dans la chaîne transmise au constructeur.

print(Lambda_terme('''(james
                   bond007)'''))

L'exception LambdaSyntaxError est déclenchée en cas de présence de caractères non autorisés ou de malformation syntaxique.

# Lambda_terme('bond 007')

# Lambda_terme('(james bond007 !)')

Autres constructions

Deux méthodes permettent de construire de nouveaux $\lambda$-termes à partir de $\lambda$-termes existant.

La méthode abstrait permet de construire une abstraction.

print(T1.abstrait('x'))
print(T2.abstrait('y'))

La méthode applique construit une application d'un terme sur un autre.

print(T2.applique(T3))
print(T3.applique(T2))

Quelques prédicats

Trois prédicats est_variable, est_abstraction et est_application permettent de reconnaître la nature d'un $\lambda$-terme.

# pour rappel des termes définis
for t in termes:
    print(t)

tuple(t.est_variable() for t in termes)

tuple(t.est_abstraction() for t in termes)

tuple(t.est_application() for t in termes)

Variables libres, variables liées

Parmi les variables figurant dans un $\lambda$-terme, certaines sont dites libres, et d'autres liées.

Les variables libres sont celles qui ne sont pas sous la portée d'une abstraction. L'ensemble FV(T) des variables libres d'un $\lambda$-terme T est défini inductivement par les trois règles :

FV(x) = \{x\}.
FV(\lambda x.T) = FV(T)\setminus\{x\}.
FV((T_1\ T_2)) = FV(T_1)\cup FV(T_2).

Les variables liées sont celles qui sont sous la portée d'une abstraction. L'ensemble BV(T) des variables liées d'un $\lambda$-terme T est défini inductivement par les trois règles :

BV(x) = \emptyset.
BV(\lambda x.T) = BV(T)\cup \{x\} si x\in FV(T), sinon BV(\lambda x.T) = BV(T).
BV((T_1\ T_2)) = BV(T_1)\cup BV(T_2).

La méthode variables donne sous un couple constitué de l'ensemble des variables libres et de l'ensemble des variables liées du $\lambda$-terme.

tuple(t.variables() for t in termes)

Remarque : Dans un $\lambda$-terme, une variable peut être à la fois libre et liée comme le montre l'exemple du terme T5 qui contient deux occurrences de la variable x, la première étant liée et la seconde libre. Pour être plus précis, on devrait plutôt parler d'occurrence libre ou liée d'une variable.

Un $\lambda$-terme sans variable libre est appelé terme clos, ou encore combinateur.

Sous-termes

Hormis les variables, les $\lambda$-termes sont construits à partir d'autres $\lambda$-termes qui eux-mêmes peuvent être construits à l'aide d'autres $\lambda$-termes encore.

Un $\lambda$-terme contient donc des sous-termes.

Voici comment l'ensemble ST des sous-termes d'un $\lambda$-terme est défini inductivement selon la structure de ce terme.

Les variables n'ont qu'un seul sous-terme : elles-mêmes. ST(x) = \{x\}.
Les sous-termes d'une abstraction sont, outre l'abstration elle-même, les sous-termes de son corps. ST(\lambda x.T) = \{\lambda x.T\}\cup ST(T).
Les sous-termes d'une application sont, outre l'application elle-même, les sous-termes des deux termes la composant. ST((T_1\ T_2)) = \{(T_1\ T_2)\}\cup ST(T_1)\cup ST(T_2).

La méthode sous_termes donne la liste des sous-termes d'un $\lambda$-terme. L'ordre dans lequel figurent les sous-termes dans cette liste est l'ordre d'apparition de ces sous-termes dans une lecture de gauche à droite (autrement dit, un ordre préfixe).

for t in T5.sous_termes():
    print(t)

$\beta$-réduction ou calculer avec des $\lambda$-termes

Substitution

Étant donnés deux $\lambda$-termes T et R, et une variable x, on note T[x:= R] le $\lambda$-terme obtenu en substituant le terme R à toutes les occurrences libres de la variable x dans le terme T.

Si T est une variable, T[x:=R] = R si T=x et T[x := R] = T si T\neq x.
Si T=(T_1\ T_2) est une application, T[x:=R] = (T_1[x:=R]\ T_2[x := R]).
Si T=\lambda y.S est une abstraction, alors il faut distinguer deux cas pour définir T[x:=R]
- si y\not\in FV(R), alors T[x:=R] = \lambda y.S[x:= R].
- si y\in FV(R), alors T[x:=R] = \lambda z.S[y:=z][x:=R], la variable z étant une nouvelle variable n'apparaissant pas dans S ni dans R. On procède à un renommage de la variable d'abstraction ($y$) pour éviter que les occurrences libres de y de R n'entrent sous la portée de l'abstraction.

La méthode subs renvoie le terme obtenu en substituant un $\lambda$-terme à toutes les occurrences libres d'une variable.

# substitution dans une variable
print('T1 = {:s}'.format(str(T1)))
x = 'y'; R = Lambda_terme('(y x)')
print('T1[{:s}:={:s}] = {:s}'.format(x, str(R), str(T1.subs(x, R))))
x = 'x'
print('T1[{:s}:={:s}] = {:s}'.format(x, str(R), str(T1.subs(x, R))))

# substitution dans une application
print('T2 = {:s}'.format(str(T2)))
x = 'y'; R = Lambda_terme('(y x)')
print('T2[{:s}:={:s}] = {:s}'.format(x, str(R), str(T2.subs(x, R))))
x = 'x'
print('T2[{:s}:={:s}] = {:s}'.format(x, str(R), str(T2.subs(x, R))))

# substitution dans une abstraction
print('T4 = {:s}'.format(str(T4)))
x = 'x'; R = Lambda_terme('(y z)')
print('T4[{:s}:={:s}] = {:s}'.format(x, str(R), str(T4.subs(x, R))))
x = 'y'; R = Lambda_terme('(y z)')
print('T4[{:s}:={:s}] = {:s}'.format(x, str(R), str(T4.subs(x, R))))
x = 'y'; R = Lambda_terme('(y x)')
print('T4[{:s}:={:s}] = {:s}'.format(x, str(R), str(T4.subs(x, R))))

Remarque : on peut utiliser la substitution pour construire des $\lambda$-termes à partir d'autres existants.

print(Lambda_terme('(!z.(T2 T3) T4)').subs('T2', T2).subs('T3', T3).subs('T4', T4))

Réduire un terme

L'idée principale qui motive la notion de réduction est qu'une abstraction \lambda x.T représente une fonction x \mapsto T, et qu'une application d'une abstraction à un terme R, (\lambda x.T\ R) représente l'application de la fonction au terme R.

De la même façon que l'application la fonction x\mapsto x^2+2x -1 à un nombre y se ramène au calcul de l'expression y^2+2y-1 obtenue en substituant y à x, l'application (\lambda x.T\ R) doit se réduire au terme T[x:=R].

Un terme de la forme (\lambda x.T\ R), autrement dit une application d'une abstraction à un terme, est appelé redex.

La réduction d'un redex est une relation, notée \rightarrow_\beta, est définie par

 (\lambda x.T\ R) \rightarrow_\beta T[x:=R].

On peut étendre cette notion de réduction à tout $\lambda$-terme dont l'un au moins de ses sous-termes est un redex. Le terme réduit correspondant étant celui obtenu en remplaçant un sous-terme redex par son réduit.

Selon cette définition, seuls les $\lambda$-termes ayant au moins un redex parmi leurs sous-termes peuvent être réduits. Les $\lambda$-termes ne contenant aucun redex sont dit irréductibles ou encore sont des formes normales.

La méthode est_redex permet de distinguer les $\lambda$-termes qui sont des redex.

for t in termes:
    print(t, t.est_redex())

T6 = T4.applique(T5)
for t in T6.sous_termes():
    print(t, t.est_redex())

La méthode reduit réduit les redex. La valeur de l'expression T.reduit() est un couple (Lambda_terme, bool) dont la valeur dépend du $\lambda$-terme T :

si T contient un redex, alors le booléen a la valeur True et la première composante du couple est le $\lambda$-terme obtenu en remplaçant le redex le plus à gauche dans T par le terme obtenu par une étape de réduction.
si T ne contient aucun redex, alors le couple est (T, False).

t, reduit = T2.reduit()
print(T2)
print(reduit)
print(t)

T7, reduit = T6.reduit()
print(T6)
print(reduit)
print(T7)

Le terme T6 contient deux redex. Comme il a été signalé la méthode reduit réduit le redex le plus à gauche, et dans le cas de T6 le redex le plus à gauche est T6 lui-même. Et cela donne le terme T7.

Mais comme T6 = (T4 T5), et que T5 est un redex, considérons le terme (T4 T5') dans lequel T5' est le terme obtenu en réduisant le redex T5.

T5bis, reduit = T5.reduit()
T7bis = T4.applique(T5bis)
print(T5)
print
print(T7bis)

Nous voyons donc qu'un $\lambda$-terme peut se réduire de plusieurs façons (en fait d'autant de façon que le terme contient de sous-termes qui sont des redex).

En particulier nous avons

T6 \rightarrow_\beta T7 et
T6 \rightarrow_\beta T7bis.

Si nous envisageons les \beta reductions comme des étapes de calcul, nous avons donc deux voies distinctes pour « calculer » T6.

Poursuivons le calcul pour chacun des deux termes T7 et T7bis qui ne sont pas des formes normales.

T8, _ = T7.reduit()
T8bis, _ = T7bis.reduit()
print('{} = {} : {}'.format(str(T8), str(T8bis), T8==T8bis))

Après une nouvelle étape de réduction nous obtenons le même terme ((x\ y)\ y) qui est irréductible. On peut dire que par deux calculs différents T6 se calcule, ou se normalise, en ((x\ y)\ y). On écrit

 \mathtt{T6} \twoheadrightarrow_{\beta} ((x\ y)\ y),

la notation T\twoheadrightarrow_{\beta} R signifiant qu'il y a un nombre quelconque (y compris nul) d'étapes de $\beta$-réduction pour arriver au terme R en partant de T (dit en terme plus savant, la relation \twoheadrightarrow_\beta est la clôture réflexive et transitive de la relation $\rightarrow_\beta$).

Formes normales, normalisation

On dit d'un $\lambda$-terme T qu'il est normalisable s'il existe un $\lambda$-terme R irréductible tel que

 T\twoheadrightarrow_{\beta} R.

Dans ce cas, on dit que R est une forme normale de T.

Par exemple, T6 est normalisable et admet ((x\ y)\ y) pour forme normale.

Deux questions se posent naturellement :

est-ce que tout $\lambda$-terme est normalisable ?
un $\lambda$-terme normalisable peut-il avoir plusieurs formes normales ?

La réponse à la première question est négative. Il suffit pour s'en convaincre de considérer le terme

\Omega = (\lambda x.(x\ x)\ \lambda x.(x\ x)),

qui est un redex et est donc réductible.

OMEGA = Lambda_terme('(!x.(x x) !x.(x x))')
print(OMEGA)
t, reduit = OMEGA.reduit()
print(reduit)
print('{} -> {}'.format(str(OMEGA), str(t)))
print(t==OMEGA)

Le terme \Omega n'a qu'un seul redex. Il n'y a donc qu'une seule façon de le réduire et cette réduction donne le terme \Omega lui-même. Quelque soit le nombre d'étapes de réduction qu'on effectue on garde toujours le même terme : \Omega n'est donc pas normalisable.

Il existe donc des termes non normalisables, et \Omega en est un exemple les plus simples.

Venons-en maintenant à la deuxième question : un terme normalisable peut-il avoir plusieurs formes normales ?

Cette question est naturelle puisque lorsqu'un $\lambda$-terme possède plusieurs redex, il y a plusieurs façons de le réduire, et il se pourrait bien que ces voies différentes mènent à des formes normales différentes.

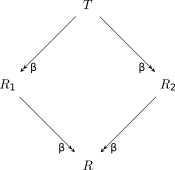
Cela n'a pas été le cas pour le terme T6. Et il se trouve que cet exemple particulier reflète la situation générale, car la relation de $\beta$-réduction satisfait une propriété qu'on appelle propriété du diamant.

Propriété du diamant Soit T un $\lambda$-terme qui peut se réduire en un nombre fini d'étapes en deux termes différents R_1 et R_2. Alors il existe un terme R en lequel chacun des deux termes R_1 et R_2 se réduit en un nombre quelconque (y compris nul) d'étapes.

Cette propriété doit son nom à la figure qui l'illustre. Cette propriété est aussi connue sous le nom de confluence de la $\beta$-réduction.

Conséquence de la propriété du diamant : Un $\lambda$-terme normalisable ne peut avoir qu'une seule forme normale.

Maintenant que nous avons répondu aux deux questions que nous nous sommes posées, il en vient une troisième.

Étant donné que certains $\lambda$-termes sont normalisables et d'autres non, y a-t-il un moyen de les reconnaître ?

Si par moyen nous entendons un algorithme général prenant un $\lambda$-terme en entrée, et répondant OUI si ce terme est normalisable et NON dans le cas contraire, alors la réponse est non. Aucun algorithme ne permet de distinguer les termes normalisables de ceux qui ne le sont pas. Le problème de la reconnaissance des termes normalisables est indécidable.

Dit en d'autres termes, l'ensemble des termes normalisables n'est pas récursif. En revanche il est récursivement énumérable. En effet, si un terme est normalisable, pour s'en rendre compte il suffit de suivre tous les chemins de réduction. L'un d'eux mène à un terme irréductible et on le trouvera en un nombre fini d'étapes.

La méthode forme_normale calcule la forme normale d'un terme normalisable si ce terme l'est, et ne renvoie rien dans le cas contraire.

print(T6.forme_normale())

print(OMEGA.forme_normale())

Hmmmm ... Comment est-ce possible puisque nous venons de voir qu'aucun algorithme ne permet de décider si un terme est normalisable ?

En fait le nombre d'étapes de réduction dans le calcul d'une forme normale est limité (par défaut à 100 étapes maximum). On peut visualiser chaque étape de calcul avec le paramètre optionnel verbose auquel il faut attribuer la valeur True.

T6.forme_normale(verbose=True)

On voit que la forme normale du terme T6 est calculé en trois étapes.

Pour un terme non normalisable les calculs peuvent (en principe) être infinis. Voici la tentative de détermination d'une forme normale pour le terme \Omega limité à dix étapes à l'aide du paramètre optionnel nb_etapes_max.

OMEGA.forme_normale(verbose=True, nb_etapes_max=10)

$\beta$-équivalence

La relation \twoheadrightarrow_\beta n'est pas symétrique. En effet, en général, si T\twoheadrightarrow_\beta R, on n'a pas R\twoheadrightarrow_\beta T.

En considèrant que la forme normale d'un terme normalisable représente sa « valeur », on peut définir une relation d'équivalence sur les $\lambda$-termes normalisables. Cette relation d'équivalence est la clôture symétrique de la relation de réduction \twoheadrightarrow_\beta.

Deux $\lambda$-termes T et S (normalisables ou non) sont dit $\beta$-équivalents, et on note T=_\beta S, s'il existe un terme R tel que T\twoheadrightarrow_\beta R et S\twoheadrightarrow_\beta R.

Ainsi deux termes normalisables ayant la même forme normale sont $\beta$-équivalents.

Théorème du point fixe Pour tout $\lambda$-terme T, il existe un $\lambda$-terme X tel que

 (T\ X) =_\beta X.

La démonstration de ce théorème se fait en considérant les $\lambda$-termes

 W = \lambda x.(T\ (x\ x)),

 X = (W\ W).

Il est clair que

 X \rightarrow_\beta (T\ (W\ W)) = (T\ X),

et donc que

 X =_\beta (T\ X).

W = Lambda_terme('!x.(T (x x))')
X = W.applique(W)
print(X)
print(X.reduit()[0])

Remarque À noter que dans la démonstration du théorème du point fixe, pour établir que (T\ X) =_\beta X, on a montré que X se réduit en (T\ X) et non le contraire.

Pouvoir d'expression du $\lambda$-calcul

Dans cette section, nous allons découvrir que le $\lambda$-calcul permet

de représenter les nombres entiers et de définir les opérations arithmétiques de base
de définir des couples, listes, structures à la base de nombreuses autres structures de données
de définir des booléens, et de simuler des expressions conditionnelles
d'itérer des fonctions,
d'exprimer n'importe quelle fonction récursive.

Bref, d'un certain point de vue le $\lambda$-calcul est un langage de programmation ... certes assez peu efficace comme on pourra s'en rendre compte.

Booléens, opérateurs logiques et conditionnelles

Les deux booléens VRAI et FAUX

On peut représenter les deux booléens VRAI et FAUX par les $\lambda$-termes

 \mathtt{VRAI} = \lambda x.\lambda y.x,

 \mathtt{FAUX} = \lambda x.\lambda y.y.

VRAI = Lambda_terme('!x.!y.x')
FAUX = Lambda_terme('!x.!y.y')

Remarque les deux termes \mathtt{VRAI} et \mathtt{FAUX} sont termes clos irréductibles.

Le terme IF

Ce choix peut être justifiée a posteriori en considérant que l'expression conditionnelle fréquente en programmation

  IF c THEN a ELSE s

peut être facilement simulée à l'aide d'abstractions des variables c, a et s par le $\lambda$-terme

 \mathtt{IF} = \lambda c.\lambda a.\lambda s.((c\ a)\ s).

IF = Lambda_terme('!c.!a.!s.((c a) s)')

IF.applique(VRAI).applique(Lambda_terme('ALORS')).applique(Lambda_terme('SINON')).forme_normale(verbose=True)

IF.applique(FAUX).applique(Lambda_terme('ALORS')).applique(Lambda_terme('SINON')).forme_normale(verbose=True)

Remarque Le $\lambda$-terme \mathtt{IF} permet d'exprimer des $\lambda$-termes ayant une forme normale bien que l'une ou l'autre de ses sous-termes n'en aient pas, comme par exemple

(((\mathtt{IF}\, \mathtt{VRAI})\, \mathtt{ALORS})\, \mathtt{OMEGA}) qui se réduit en \mathtt{ALORS} (et a donc une forme normale si \mathtt{ALORS} en a une) bien que \mathtt{OMEGA} n'en ait pas ;
ou (((\mathtt{IF}\, \mathtt{FAUX})\, \mathtt{OMEGA})\, \mathtt{SINON}) qui se réduit en \mathtt{SINON}.

Cette propriété est bien utile en programmation, et servira pour la programmation de fonctions récursives.

IF.applique(VRAI).applique(Lambda_terme('ALORS')).applique(OMEGA).forme_normale(verbose=True)

IF.applique(FAUX).applique(OMEGA).applique(Lambda_terme('SINON')).forme_normale(verbose=True)

Le fait que le terme \mathtt{IF} se comporte bien comme on l'attend résulte du choix de la stratégie de réduction des redex les plus à gauche en priorité. Si la stratégie choisie avait été de réduire le redex le plus à droite, la réduction de chacun des deux termes précédents aurait conduit à la tentative de réduire le terme \Omega qui échoue puisque celui-ci n'est pas normalisable comme on l'a vu.

Il est facile de définir les opérateurs logiques de base : conjonction, disjonction et négation.

Opérateur ET

L'opérateur logique de conjonction peut être défini par

 \mathtt{ET} = \lambda a.\lambda b.(((\mathtt{IF}\ a)\ b)\ \mathtt{FAUX}).

ET = IF.applique(Lambda_terme('a')).applique(Lambda_terme('b')).applique(FAUX).abstrait('b').abstrait('a')

print(ET)

Et on peut verifier que ce terme satisfait bien à la table de vérité de l'opérateur de conjonction.

ET.applique(VRAI).applique(VRAI).forme_normale(verbose=True) == VRAI

ET.applique(VRAI).applique(FAUX).forme_normale(verbose=True) == FAUX

ET.applique(FAUX).applique(VRAI).forme_normale(verbose=True) == FAUX

ET.applique(FAUX).applique(FAUX).forme_normale(verbose=True) == FAUX

Opérateur OU

L'opérateur logique de disjonction peut être défini par

 \mathtt{OU} = \lambda a.\lambda b.(((\mathtt{IF}\ a)\ \mathtt{VRAI})\ b).

OU = IF.applique(Lambda_terme('a')).applique(VRAI).applique(Lambda_terme('b')).abstrait('b').abstrait('a')

print(OU)

Et on peut verifier que ce terme satisfait bien à la table de vérité de l'opérateur de disjonction.

OU.applique(VRAI).applique(VRAI).forme_normale(verbose=True) == VRAI

OU.applique(VRAI).applique(FAUX).forme_normale(verbose=True) == VRAI

OU.applique(FAUX).applique(VRAI).forme_normale(verbose=True) == VRAI

OU.applique(FAUX).applique(FAUX).forme_normale(verbose=True) == FAUX

Opérateur NON

L'opérateur de négation peut être défini par le terme

 \mathtt{NON} = \lambda a.(((\mathtt{IF}\ a)\ \mathtt{FAUX})\ \mathtt{VRAI}).

NON = IF.applique(Lambda_terme('a')).applique(FAUX).applique(VRAI).abstrait('a')

print(NON)

NON.applique(VRAI).forme_normale(verbose=True) == FAUX

NON.applique(FAUX).forme_normale(verbose=True) == VRAI

Entiers, successeurs, addition, multiplication et exponentiation

Numéraux de Church

Il existe plusieurs façons de représenter les entiers naturels par un $\lambda$-terme. La représentation donnée ici est connue sous le nom de numéraux de Church.

Dans le système de Church, un entier n\in\mathbb{N} est représenté par le $\lambda$-terme

 \lceil n\rceil = \lambda f.\lambda x. (f^n\ x),

dans lequel le sous-terme (f^n\ x) est un raccourci pour signifier

 (f^n\ x) = (f\ (f\ (\ldots (f\ x)\ldots))),

terme dans lequel f apparaît n fois. En quelque sorte le terme représentant l'entier n est une représentation unaire de n.

Ainsi on a

\begin{align*} \lceil 0\rceil &= \lambda f.\lambda x.x\ \lceil 1\rceil &= \lambda f.\lambda x.(f\ x)\ \lceil 2\rceil &= \lambda f.\lambda x.(f\ (f\ x))\ \lceil 3\rceil &= \lambda f.\lambda x.(f\ (f\ (f\ x))). \end{align*}

Le $\lambda$-terme \lceil n\rceil est donc un terme capable d'appliquer n fois une fonction F sur une donnée X. En effet on a

 (\lceil n\rceil\ F) \twoheadrightarrow_\beta \lambda x.(F\ldots(F\ x)),

 ((\lceil n\rceil\ F)\ X) \twoheadrightarrow_\beta (F\ldots(F\ X)).

ZERO = Lambda_terme('!f.!x.x')

UN = Lambda_terme('!f.!x.(f x)')

DEUX = Lambda_terme('!f.!x.(f (f x))')

Le calcul ci-dessous vérifie bien qu'un numéral appliqué à un terme résulte en une fonction itération du terme.

DEUX.applique(Lambda_terme('F')).forme_normale(verbose=True)

Remarque les numéraux de Church sont des $\lambda$-termes clos irréductibles.

Successeur

Lorsqu'on a compris que pour tout numéral \lceil n\rceil on a

 ((\lceil n\rceil\ F)\ X) \twoheadrightarrow_\beta (F\ldots(F\ X)),

alors il est facile de concevoir un $\lambda$-terme \mathtt{SUC} tel que

 (\mathtt{SUC}\ \lceil n\rceil) =_\beta \lceil n+1\rceil.

SUC = Lambda_terme('!n.!f.!x.(f ((n f) x))')

print(SUC)

TROIS = SUC.applique(DEUX).forme_normale(verbose=True)

La fonction qui suit permet d'obtenir le numéral de Church correspondant à un entier naturel (de Python).

def int_en_church(n):
    if n == 0:
        return ZERO
    else:
        return SUC.applique(int_en_church(n - 1)).forme_normale()

for n, t in enumerate((ZERO, UN, DEUX, TROIS)):
    print(int_en_church(n) == t)

Addition

En appliquant trois fois de suite le terme \mathtt{SUC} sur le terme \lceil 2\rceil on obtient un terme dont la forme normale est le numéral \lceil 5\rceil.

TROIS.applique(SUC).applique(DEUX).forme_normale(verbose=True) == int_en_church(5)

Ainsi on peut définir un $\lambda$-terme \mathtt{ADD} qui appliqué à deux numéraux est $\beta$-équivalent au numéral somme. En définissant donc

 \mathtt{ADD} = \lambda n.\lambda m.((n\ \mathtt{SUC})\ m),

on a

 ((\mathtt{ADD}\ \lceil n\rceil)\ \lceil m\rceil) =_\beta \lceil n+m\rceil.

M_ADD = Lambda_terme('!n.!m.((n SUC) m)')
ADD = M_ADD.subs('SUC', SUC)

print(ADD)

QUATRE = ADD.applique(UN).applique(TROIS).forme_normale(verbose=True)

CINQ = ADD.applique(TROIS).applique(DEUX).forme_normale(verbose=True)

SEPT = ADD.applique(QUATRE).applique(TROIS).forme_normale(verbose=True)

Multiplication

On pourrait définir un terme pour la multiplication en considérant que multiplier n par m c'est répéter n fois l'addition de m à partir de 0.

M_MUL = Lambda_terme('!n.!m.((n (ADD m)) ZERO)')
MUL = M_MUL.subs('ADD', ADD).subs('ZERO', ZERO)
print(MUL)

MUL.applique(DEUX).applique(TROIS).forme_normale(verbose=True) == int_en_church(6)

Mais il s'avère plus simple (et plus efficace comme on pourra le constater) de définir le terme \mathtt{MUL} par

 \mathtt{MUL} = \lambda n.\lambda m.\lambda f.(n\ (m\ f)).

En effet, il est clair que

 ((\mathtt{MUL} \lceil n\rceil)\ \lceil m\rceil) \twoheadrightarrow_\beta \lambda f.(\lceil n\rceil\ (\lceil m\rceil\ f)),

et le terme obtenu est la répétition m fois du terme f, répétition répétée elle-même n fois. Au bilan le terme f est répété n\times m fois.

Et on a donc bien

 ((\mathtt{MUL} \lceil n\rceil)\ \lceil m\rceil) =_\beta \lceil n\times m\rceil.

MUL = Lambda_terme('!n.!m.!f.(n (m f))')

SIX = MUL.applique(DEUX).applique(TROIS).forme_normale(verbose=True)

Le calcul de la forme normale de ((\mathtt{MUL}\ \lceil 2\rceil)\ \lceil 3\rceil) avec cette version de \mathtt{MUL} est bien plus court que le calcul effectué avec la version précédente.

Exponentiation

Comme pour la multiplication, on pourrait envisager de définir un terme pour l'exponentiation en considérant qu'il suffit de répéter m fois le terme \mathtt{MUL} appliqué à n pour obtenir un terme qui se réduirait au numéral représentant n^m.

Mais il est possible de définir un terme beaucoup plus simple :

 \mathtt{EXP} = \lambda n.\lambda m.(m\ n).$

```python
EXP = Lambda_terme('!n.!m.(m n)')
```

```python
HUIT = EXP.applique(DEUX).applique(TROIS).forme_normale(verbose=True)
```

```python
HUIT == int_en_church(8)
```

```python
NEUF = EXP.applique(TROIS).applique(DEUX).forme_normale(verbose=True)
```

```python
NEUF == int_en_church(9)
```

#### Nullité


Considérons le terme $((\lceil n\rceil\ \lambda x.\mathtt{FAUX})\ \mathtt{VRAI})$. Si $n=0$ on a 
$$((\lceil 0\rceil\ \lambda x.\mathtt{FAUX})\ \mathtt{VRAI}) \twoheadrightarrow_\beta (\lambda x.x\ \mathtt{VRAI}) \rightarrow_\beta \mathtt{VRAI}.$$
Et si $n\neq 0$ on a
$$((\lceil n\rceil\ \lambda x.\mathtt{FAUX})\ \mathtt{VRAI}) \twoheadrightarrow_\beta (\lambda x.\mathtt{FAUX}\ \mathtt{VRAI}) \rightarrow_\beta \mathtt{FAUX}.$$

Avec une abstraction, on obtient le $\lambda$-terme 
$$ \mathtt{NUL} = \lambda n.(),$$
tel que pour $n=0$
$$ (\mathtt{NUL}\ \lceil 0\rceil) =_\beta \mathtt{VRAI},$$
et pour $n\neq 0$
$$ (\mathtt{NUL}\ \lceil n\rceil) =_\beta \mathtt{FAUX}.$$

En d'autres termes, le $\lambda$-terme $\mathtt{NUL}$ correspond à un prédicat permettant de tester la nullité d'un entier.

```python
M_NUL = Lambda_terme('!n.((n !x.FAUX) VRAI)')
print(M_NUL)
NUL = M_NUL.subs('FAUX', FAUX).subs('VRAI', VRAI)
print(NUL)
```

```python
NUL.applique(ZERO).forme_normale(verbose=True) == VRAI
```

```python
NUL.applique(TROIS).forme_normale(verbose=True) == FAUX
```

**Remarque** Arrivé à ce stade, il nous manque une opération arithmétique de base : la soustraction, et la possibilité de comparaison plus générale permettant de décider si un entier est inférieur à un autre. Ce manque sera comblé une fois que nous aurons vu une représentation des couples.


### Couples et listes


#### Constructeur et sélecteurs de couples


Comment exprimer un couple de $\lambda$-termes à l'aide d'un $\lambda$-terme ? Une fois ce couple exprimé comment en extraire chacune des deux composantes ? 


Soient $M$ et $N$ deux $\lambda$-termes quelconques. Considérons les deux termes $((\mathtt{VRAI}\ M)\ N)$ et $((\mathtt{FAUX}\ M)\ N)$. Il est facile de vérifier que
$$ ((\mathtt{VRAI}\ M)\ N) =_\beta M,$$
et
$$ ((\mathtt{FAUX}\ M)\ N) =_\beta N.$$

On déduit de ce constat que 
$$[M, N] = \lambda s.((s\ M)\ N)$$
est un $\lambda$-terme pouvant représenter le couple $(M, N)$ et que la sélection de l'une ou l'autre des deux composantes peut se faire en appliquant le terme sur l'un ou l'autre des deux termes $\mathtt{VRAI}$ ou $\mathtt{FAUX}$ :

$$ ([M, N]\ \mathtt{VRAI}) =_\beta M,$$
et
$$ ([M, N]\ \mathtt{FAUX}) =_\beta N.$$


Ces considérations amènent à définir le terme constructeur de couple $\mathtt{CONS}$
$$ \mathtt{CONS} = \lambda x.\lambda y.\lambda s.((s\ x)\ y),$$
ainsi que les deux sélecteurs $\mathtt{CAR}$, pour accéder à la première composante, et $\mathtt{CDR}$, pour accéder à la deuxième composante
$$\mathtt{CAR} = \lambda c.(c\ \mathtt{VRAI}),$$
et
$$\mathtt{CDR} = \lambda c.(c\ \mathtt{FAUX}).$$

```python
CONS = Lambda_terme('!x.!y.!s.((s x) y)')
print(CONS)
```

```python
UN_DEUX = CONS.applique(UN).applique(DEUX).forme_normale(verbose=True)
```

```python
M_CAR = Lambda_terme('!c.(c VRAI)')
print(M_CAR)
CAR = M_CAR.subs('VRAI', VRAI)
print(CAR)
```

```python
CAR.applique(UN_DEUX).forme_normale(verbose=True) == UN
```

```python
M_CDR = Lambda_terme('!c.(c FAUX)')
print(M_CDR)
CDR = M_CDR.subs('FAUX', FAUX)
print(CDR)
```

```python
CDR.applique(UN_DEUX).forme_normale(verbose=True) == DEUX
```

```python
M = Lambda_terme('M')
CPLE_M = CONS.applique(CAR.applique(M)).applique(CDR.applique(M))
```

```python
CDR.applique(CPLE_M).forme_normale(verbose=True)
```

**Remarques** 
1. le terme $((\mathtt{CONS}\ M)\ N)$ est clos si et seulement si $M$ et $N$ le sont, et il est normalisable si et seulement si $M$ et $N$ le sont.

2. les noms donnés aux termes $\mathtt{CONS}$, $\mathtt{CAR}$ et $\mathtt{CDR}$ font référence aux noms donnés aux constructeurs et sélecteurs de paires dans le langage de programmation LISP (et ses successeurs comme SCHEME).


#### Prédécesseur d'un entier, soustraction


Envisageons la fonction $F$ qui, à un couple $(m, n)$ d'entiers, associe le couple $(n, n+1)$. En partant du couple $(0,0)$ et en itérant $n$ fois cette fonction, on obtient le couple $(n-1, n)$. La première composante de ce couple est l'entier $n-1$, donc l'entier qui précède $n$.

C'est l'idée de base pour définir un $\lambda$-terme $\mathtt{PRED}$ tel que pour tout entier $n\geq 1$ on ait
$$ (\mathtt{PRED}\ \lceil n\rceil) =_\beta \lceil n-1\rceil.$$

```python
M_F = Lambda_terme('!c.((CONS (CDR c)) (SUC (CDR c)))')
print(M_F)
F = M_F.subs('CONS', CONS).subs('CDR', CDR).subs('SUC', SUC)
print(F)
```

```python
QUATRE.applique(F).applique(CONS.applique(ZERO).applique(ZERO)).forme_normale() == CONS.applique(TROIS).applique(QUATRE).forme_normale()
```

Le $\lambda$-terme $\mathtt{PRED}$ est défini par

$$ \mathtt{PRED} = \lambda n.(\mathtt{CAR} ((n \lambda c.((\mathtt{CONS}\ (\mathtt{CDR}\ c))\ (\mathtt{SUC} (\mathtt{CDR}\ c)))) ((\mathtt{CONS}\ \mathtt{ZERO})\ \mathtt{ZERO}))).$$

```python
M_PRED = Lambda_terme('!n.(CAR ((n !c.((CONS (CDR c)) (SUC (CDR c)))) ((CONS ZERO) ZERO)))')
print(M_PRED)
PRED = M_PRED.subs('CAR', CAR).subs('CONS', CONS).subs('CDR', CDR).subs('SUC', SUC).subs('ZERO', ZERO)
print(PRED)
```

```python
PRED.applique(CINQ).forme_normale(verbose=True) == QUATRE
```

**Remarque** le terme $(\mathtt{PRED}\ \mathtt{ZERO})$ est normalisable et sa forme normale est $\mathtt{ZERO}$.

```python
PRED.applique(ZERO).forme_normale(verbose=True) == ZERO
```

Une fois le prédesseur exprimé, il est facile de définir la soustraction comme une itération du prédécesseur.

```python
M_SUB = Lambda_terme('!n.!m.((m PRED) n)')
print(M_SUB)
SUB = M_SUB.subs('PRED', PRED)
print(SUB)
```

```python
SUB.applique(TROIS).applique(UN).forme_normale(verbose=True) == DEUX
```

#### Infériorité, égalité


**Remarque** on a l'équivalence 
$$ n <= m \Longleftrightarrow ((\mathtt{SUB}\ \lceil n\rceil)\ \lceil m\rceil) =_\beta \mathtt{ZERO}.$$

```python
SUB.applique(TROIS).applique(QUATRE).forme_normale() == ZERO
```

De là vient l'idée de définir le $\lambda$-terme
$$\mathtt{INF} = \lambda n.\lambda m.(\mathtt{NUL}\ ((\mathtt{SUB}\ n)\ m)),$$
qui est tel que pour tout couple d'entier $(n, m)$, on a

* si $n \leq m$
  $$ ((\mathtt{INF}\ \lceil n\rceil)\ \lceil m\rceil) =_\beta \mathtt{VRAI},$$
* et si $n > m$
  $$ ((\mathtt{INF}\ \lceil n\rceil)\ \lceil m\rceil) =_\beta \mathtt{FAUX}.$$

```python
M_INF = Lambda_terme('!n.!m.(NUL ((SUB n) m))')
print(M_INF)
INF = M_INF.subs('NUL', NUL).subs('SUB', SUB)
print(INF)
```

```python
INF.applique(TROIS).applique(UN).forme_normale() == FAUX
```

```python
INF.applique(UN).applique(TROIS).forme_normale() == VRAI
```

```python
INF.applique(UN).applique(UN).forme_normale() == VRAI
```

Et à partir de $\mathtt{INF}$ on peut définir le terme
$$ \mathtt{EGAL} = \lambda n.\lambda m.((\mathtt{ET}\ ((\mathtt{INF}\ \lceil n\rceil)\ \lceil m\rceil))\ ((\mathtt{INF}\ \lceil m\rceil)\ \lceil n\rceil)),$$
qui est tel que pour tout couple d'entier $(n, m)$, on a

* si $n = m$
  $$ ((\mathtt{EGAL}\ \lceil n\rceil)\ \lceil m\rceil) =_\beta \mathtt{VRAI},$$
* et si $n \neq m$
  $$ ((\mathtt{EGAL}\ \lceil n\rceil)\ \lceil m\rceil) =_\beta \mathtt{FAUX}.$$

```python
M_EGAL = Lambda_terme('!n.!m.((ET ((INF n) m)) ((INF m) n))')
print(M_EGAL)
EGAL = M_EGAL.subs('ET', ET).subs('INF', INF)
print(EGAL)
```

```python
EGAL.applique(UN).applique(UN).forme_normale() == VRAI
```

```python
EGAL.applique(UN).applique(DEUX).forme_normale() == FAUX
```

#### Listes de termes


Classiquement, on peut considérer une liste de termes $ <M_1, M_2, \ldots, M_n>$ comme un couple dont la première composante est l'élément en tête de la liste, et la seconde composante est la liste des éléments qui restent :
$$ <M_1, M_2, \ldots, M_n> = [M_1, <M_2, \ldots, M_n>].$$
Ainsi une liste de trois éléments est un emboîtement de trois couples :

$$ <M_1, M_2, M_3> = [M_1, [M_2, [M3, <>]]],$$
la deuxième composante du couple le plus interne, $<>$ désignant la liste vide.

On voit bien comment construire des listes ($\mathtt{CONS}$), accéder à leur tête ($\mathtt{CAR}$) et à leur reste ($\mathtt{CDR}$).

Il reste à trouver une représentation de la liste vide et un terme permettant de distinguer la liste vide de celles qui ne le sont pas. 

Et le problème de la vacuité d'une liste va imposer de mettre une couche d'abstraction supplémentaire sur notre représentation des listes.


Étant donnés $n$ $\lambda$-termes $M_1$, $M_2$, ..., $M_n$, on peut représenter la liste de ces termes par le $\lambda$-terme

$$ <M_1, M_2, \ldots, M_n> = \lambda x.[M_1, [M_2, \ldots[M_n, <>]\ldots],$$
définition dans laquelle $<>$ désigne la liste vide qui peut être représentée par 
$$ <> = \lambda x.\lambda s.x\,\, (= \mathtt{FAUX}).$$

```python
LVIDE = Lambda_terme('!x.!s.x')
```

Le terme $\mathtt{LCONS}$ permettant d'ajouter un terme $t$ en tête d'une liste $r$ peut alors être facilement écrit de la manière suivante en utilisant $\mathtt{CONS}$.

$$ \mathtt{LCONS} = \lambda t.\lambda r.\lambda x.((\mathtt{CONS}\ t)\ r).$$

```python
M_LCONS = Lambda_terme('!t.!r.!x.((CONS t) r)')
print(M_LCONS)
LCONS = M_LCONS.subs('CONS', CONS)
print(LCONS)
```

```python
M1 = Lambda_terme('M1')
M2 = Lambda_terme('M2')
M3 = Lambda_terme('M3')
L = LCONS.applique(M1).applique(LCONS.applique(M2).applique(LCONS.applique(M3).applique(LVIDE)))
print(L.forme_normale())
```

Notons que si $L$ est une liste non vide, alors quelque soit le terme $M$, $(L\ M)$ se réduit en un couple dont la seconde composante est la liste reste de $L$. En particulier, le terme $M$ a disparu.

```python
print(L.applique(Lambda_terme('M')).forme_normale())
```

Et dans le cas de la liste vide, $(\mathtt{LVIDE}\ M)$ se réduit en $\lambda s.M$.

```python
print(LVIDE.applique(Lambda_terme('M')).forme_normale())
```

Les deux remarques précédentes sont à la base de la définition des sélecteurs $\mathtt{LCAR}$ et $\mathtt{LCDR}$ présentés maintenant.


Le sélecteur $\mathtt{LCAR}$ permettant d'obtenir l'élément de tête d'une liste est construit en utilisant $\mathtt{CAR}$.

$$ \mathtt{LCAR} = \lambda l.(\mathtt{CAR}\ (l\ \mathtt{VRAI})).$$

```python
M_LCAR = Lambda_terme('!l.(CAR (l VRAI))')
print(M_LCAR)
L_CAR = M_LCAR.subs('CAR', CAR).subs('VRAI', VRAI)
print(L_CAR)
```

```python
L_CAR.applique(L).forme_normale(verbose=True) == Lambda_terme('M1')
```

Notons que 
$$(\mathtt{LCAR}\ \mathtt{LVIDE}) \twoheadrightarrow_\beta \mathtt{LVIDE}.$$ 

```python
L_CAR.applique(LVIDE).forme_normale(verbose=True)  == LVIDE
```

Le sélecteur $\mathtt{LCDR}$ permettant d'obtenir le reste d'une liste se définit à l'aide de $\mathtt{CDR}$.

$$ CDR = \lambda l.(\mathtt{CDR}\ (l\ \mathtt{VRAI})).$$

```python
M_LCDR = Lambda_terme('!l.(CDR (l VRAI))')
print(M_LCDR)
LCDR = M_LCDR.subs('CDR', CDR).subs('VRAI', VRAI)
print(LCDR)
```

```python
LCDR.applique(L).forme_normale(verbose=True)
```

Notons que 
$$(\mathtt{LCDR}\ \mathtt{LVIDE}) \twoheadrightarrow_\beta \mathtt{LVIDE}.$$ 

```python
LCDR.applique(LVIDE).forme_normale(verbose=True) == LVIDE
```

Le terme qui permet de distinguer une liste vide d'une liste qui ne l'est pas est

$$ \mathtt{LESTVIDE} = \lambda l.((l\ \mathtt{VRAI})\ \lambda t.\lambda r.\mathtt{FAUX}).$$

```python
M_LESTVIDE = Lambda_terme('!l.((l VRAI) !t.!r.FAUX)')
print(M_LESTVIDE)
LESTVIDE = M_LESTVIDE.subs('VRAI', VRAI).subs('FAUX', FAUX)
```

```python
LESTVIDE.applique(LVIDE).forme_normale(verbose=True) == VRAI
```

```python
LESTVIDE.applique(L).forme_normale(verbose=True) == FAUX
```

### Itération


On l'a vu à plusieurs occasions ($\mathtt{ADD}$, $\mathtt{MUL}$, $\mathtt{EXP}$, $\mathtt{NUL}$, $\mathtt{SUB}$), les numéraux de Church permettent d'itérer l'application d'un terme.


Étudions encore un cas d'école avec la classique fonction factorielle qui peut se programmer en Python à l'aide d'une boucle `for`.

~~~python
def fact(n):
    f = 1
    for i in range(n+1):
        f = f*i
    return f
~~~


Ce programme utilise deux variables $\mathtt{i}$ et $\mathtt{f}$.

Si on ajoute la valeur fictive 0 pour la variable $\mathtt{i}$ avant la boucle `for`, le couple ($\mathtt{i}$, $\mathtt{f}$) prend les valeurs successives : (0, 1), (1, 1), (2, 2), (3, 6), ..., ($n$, $n!$). Ainsi à chaque étape de l'itération le couple est transformé selon la règle :

$$ (i, f) \rightarrow (i+1, f\times i).$$

C'est cette règle qui est itérée $n$ fois. Et cette règle peut être représentée par un $\lambda$-terme transformant un couple $[\lceil i\rceil, \lceil f\rceil]$ en le couple $[\lceil i+1\rceil, \lceil f\times i\rceil]$.


Ce qui peut être fait par 

$$ \mathtt{FACT} = \lambda n.(CDR\ ((n\ \lambda c.[(SUC\ (CAR\ c)), ((MUL\ (CAR\ c))\ (CDR\ c))])\ [ZERO, ZERO])).$$


Voici une réalisation de ce terme (que nous nommons $\mathtt{FACTv1}$ puisque d'autre réalisations de $\mathtt{}$ seront envisagées dans la suite).

```python
M_FACTv1 = Lambda_terme('!n.(CDR ((n !c.((CONS (SUC (CAR c))) ((MUL (SUC (CAR c))) (CDR c)))) ((CONS ZERO) UN)))')
print(M_FACTv1)
FACTv1 = M_FACTv1.subs('CONS', CONS).subs('CAR', CAR).subs('CDR', CDR).subs('SUC', SUC).subs('MUL', MUL).subs('UN', UN).subs('ZERO', ZERO)
print(FACTv1)
```

```python
FACTv1.applique(ZERO).forme_normale() == UN
```

```python
FACTv1.applique(UN).forme_normale() == UN
```

```python
FACTv1.applique(DEUX).forme_normale() == DEUX
```

Pour calculer $(\mathtt{FACTv1}\ \mathtt{TROIS})$, il faut au moins 309 étapes de réduction.

```python
FACTv1.applique(TROIS).forme_normale(nb_etapes_max=309) == SIX
```

Et pour  (𝙵𝙰𝙲𝚃𝚟𝟷 QUATRE), il en faut au moins 1284.

```python
FACTv1.applique(QUATRE).forme_normale(nb_etapes_max=1284) == MUL.applique(QUATRE).applique(SIX).forme_normale()
```

En suivant le principe qui a conduit à écrire le terme $\mathtt{FACTv1}$, on comprend que n'importe quelle fonction qui peut être programmée (en Python, ou tout autre langage) peut être représentée par un $\lambda$-terme.


### Et la récursivité ? Et les boucles `while` ? 


Dernier point de notre exploration du pouvoir d'expression du $\lambda$-calcul qui achèvera (peut-être) de nous convaincre que c'est un langage de programmation : peut-on représenter des fonctions récursives ? peut-on représenter des fonctions dont l'algorithme nécessite une boucle `while` ?


#### Exprimer la récursivité sans nom ?


Prenons encore la fonction factorielle comme exemple classique de fonction récursive. En Python on peut l'écrire de la façon suivante

~~~python
def fact(n):
    if n == 0:
        return 1
    else:
        return n * fact(n - 1)
~~~

<!-- #region -->
En examinant le code de cette version récursive de la fonction factorielle, on s'aperçoit que nous disposons de tous les ingrédients pour écrire un $\lambda$-terme analogue. Le voici :

$$ \mathtt{FACT} = \lambda n.(((\mathtt{IF}\ (\mathtt{NUL}\ n))\ \lceil 1\rceil)\ ((\mathtt{MUL}\ n)\ (\mathtt{FACT}\ (\mathtt{PRED}\ n)))).$$


Hmmm ... Trop facile ! Il y a un hic !
Ce terme n'est pas valide car dans le terme désigné par le nom $\mathtt{FACT}$, il y a le nom $\mathtt{FACT}$, et en $\lambda$-calcul les seuls noms intervenants dans les $\lambda$-termes sont les variables. Donc le nom $\mathtt{FACT}$ dans le $\lambda$-terme ci-dessus est juste une variable et n'est pas le $\lambda$-terme nommé $\mathtt{FACT}$. 
<!-- #endregion -->

En programmation on dit souvent d'une fonction qu'elle est récursive lorsqu'elle fait appel à elle-même, comme le fait la fonction `fact` ci-dessus. Et l'appel à une fonction se fait par le nom de cette fonction.

Comme en $\lambda$-calcul, il n'y a pas de nom, il semble, en apparence, que la définition de $\lambda$-termes suivant un schéma récursif soit impossible.

On va voir qu'il n'en est rien.


#### Avec une couche d'abstraction supplémentaire


Dans l'essai de $\lambda$-terme pour définir $\mathtt{FACT}$, remplaçons le nom $\mathtt{}$ par une variable, $f$ par exemple, et ajoutons une couche d'abstraction sur cette variable afin qu'elle soit liée. Nous obtenons un terme que nous nommerons $\Phi_{fact}$.

$$ \Phi_{fact} = \lambda f.\lambda n.(((\mathtt{IF}\ (\mathtt{NUL}\ n))\ \lceil 1\rceil)\ ((\mathtt{MUL}\ n)\ (f\ (\mathtt{PRED}\ n)))).$$

Ce $\lambda$-terme est parfaitement valide. 

Mais, compte-tenu de la couche d'abstraction supplémentaire, ce n'est certainement pas un terme candidat pour être le terme $\mathtt{FACT}$ que nous recherchons.

```python
M_PHI_FACT = Lambda_terme('!f.!n.(((IF (NUL n)) UN) ((MUL n) (f (PRED n))))')
print(M_PHI_FACT)
PHI_FACT = M_PHI_FACT.subs('IF', IF).subs('NUL', NUL).subs('UN', UN).subs('MUL', MUL).subs('PRED', PRED)
print(PHI_FACT)
```

En fait pour envisager d'utiliser ce terme pour calculer des factorielles, il faut d'abord l'appliquer à un terme (une fonction) $f$ puis appliquer à un entier (de Church). Autrement dit suivre le schéma

$$((\Phi_{fact}\ f)\ \lceil n\rceil).$$

Mais quel terme (ou fonction) $f$ utiliser ?


Et si on commençait par une fonction (un peu bizarre) nulle part définie, ou dit en termes plus $\lambda$-calculesque, par un terme dont aucune application ne possède une forme normale :

$$ \mathtt{BOTTOM} = \lambda y.\Omega,$$
où, pour rappel, $\Omega = (\lambda x.(x\ x)\ \lambda x.(x\ x))$ qui, comme on l'a vu, n'est pas normalisable. 

Il est clair que pour n'importe quel terme $M$, on a

$$(\mathtt{BOTTOM}\ M) \rightarrow_\beta\Omega\rightarrow_\beta\Omega\rightarrow_\beta\ldots.$$

```python
BOTTOM = Lambda_terme('!y.OMEGA').subs('OMEGA', OMEGA)
print(BOTTOM)
```

```python
BOTTOM.applique(Lambda_terme('M')).forme_normale(verbose=True, nb_etapes_max=3)
```

Appliquons notre terme $\Phi_{fact}$ à $\mathtt{BOTTOM}$,

```python
F1 = PHI_FACT.applique(BOTTOM)
```

et appliquons ensuite le terme obtenu à des entiers de Church.

```python
F1.applique(ZERO).forme_normale() == UN
```

```python
F1.applique(UN).forme_normale(verbose=True, nb_etapes_max=20) 
```

Le terme $F_1$ appliqué à $\lceil 0\rceil$ donne $\lceil 1\rceil$. Mais, l'application à tout autre entier de Church n'est pas normalisable.

Autrement dit la fonction représentée par $F_1$ calcule bien $0! = 1$, ... et c'est tout. C'est tout de même mieux que $\mathtt{BOTTOM}$ !

Continuons et définissons $F_2 = (\Phi_{fact}\ F_1)$.

```python
F2 = PHI_FACT.applique(F1)
```

```python
F2.applique(ZERO).forme_normale() == UN
```

```python
F2.applique(UN).forme_normale() == UN
```

```python
F2.applique(DEUX).forme_normale()
```

Le terme $F_2$ appliqué à $\lceil n\rceil$, avec $n=0\mbox{ ou }1$ donne bien $\lceil n!\rceil$. Mais pour tout autre entier l'application n'est pas normalisable. On progresse.

En fait si on définit la suite de termes $F_n$ par récurrence en posant

\begin{align}
    F_0 &= \mathtt{BOTTOM}\\
    F_1 &= (\Phi_{fact}\ F_0)\\
    F_2 &= (\Phi_{fact}\ F_1)\\
    \vdots\\
    F_{n+1} &= (\Phi_{fact}\ F_n)
\end{align}
chacun des termes de cette suite est en mesure de représenter une fonction factorielle partielle. Plus précisément, pour chaque entier $n$ on a

$$ (F_n\ \lceil k\rceil) \twoheadrightarrow_\beta \lceil k!\rceil \mbox{ si } 0\leq k < n,$$
et $(F_n\ \lceil k\rceil)$ n'est pas normalisable si $k\geq n$.


Vérifions cela sur le terme $F_4$.

```python
F4 = QUATRE.applique(PHI_FACT).applique(BOTTOM)
```

```python
F4.applique(ZERO).forme_normale() == UN
```

```python
F4.applique(UN).forme_normale() == UN
```

```python
F4.applique(DEUX).forme_normale(nb_etapes_max=244) == DEUX
```

```python
F4.applique(TROIS).forme_normale(nb_etapes_max=1510) == SIX
```

Avec le terme $\Phi_{fact}$, nous sommes en mesure de définir des fonctions « approximant » de mieux en mieux la fonction factorielle, mais le procédé itératif décrit ne permet pas d'obtenir le terme $\mathtt{FACT}$ voulu.

Remarquons néanmoins que si nous avons ce terme $\mathtt{FACT}$, alors on a

$$ (\Phi_{fact}\ \mathtt{FACT}) \rightarrow_\beta
   \lambda n.(((\mathtt{IF}\ (\mathtt{NUL}\ n))\ \lceil 1\rceil)\ ((\mathtt{MUL}\ n)\ (\mathtt{FACT}\ (\mathtt{PRED}\ n)))),$$
qui est un terme correspondant exactement à ce que nous recherchons depuis le début. De cette réduction, on peut déduire que
$$ (\Phi_{fact}\ \mathtt{FACT}) =_\beta \mathtt{FACT},$$
et cette équivalence montre que le terme $\mathtt{FACT}$ que l'on recherche est un point fixe du terme $\Phi_{fact}$. Or on a vu comment construire un terme point fixe d'un autre. 

$$\mathtt{FACT} = (\lambda x.(\Phi_{fact}\ (x\ x))\ \lambda x.(\Phi_{fact}\ (x\ x))).$$
Ce terme est un $\lambda$-terme valide qui vérifie pour tout entier $n\geq 0$
$$(\mathtt{FACT}\ \lceil n\rceil) =_\beta \lceil n!\rceil.$$

```python
W = Lambda_terme('!x.(PHIFACT (x x))').subs('PHIFACT', PHI_FACT)
FACTv2 = Lambda_terme('(W W)').subs('W', W)
print(FACTv2)
```

```python
FACTv2.applique(ZERO).forme_normale() == UN
```

```python
FACTv2.applique(UN).forme_normale() == UN
```

```python
FACTv2.applique(DEUX).forme_normale(nb_etapes_max=247) == DEUX
```

```python
FACTv2.applique(TROIS).forme_normale(nb_etapes_max=1524) == SIX
```

```python
FACTv2.applique(QUATRE).forme_normale(nb_etapes_max=10383) == int_en_church(24)
```

#### Combinateur de point fixe


Le combinateur de point fixe de Curry est défini par

$$ Y = \lambda f.(\lambda x.(f\ (x\ x))\ \lambda x.(f\ (x\ x))).$$

Il permet de construire un terme point fixe de n'importe quel terme $\Phi$, ce terme se définissant par $F = (Y\ \Phi).$. En effet,

$$ F = (Y\ \Phi) \rightarrow_\beta (\lambda x.(\Phi\ (x\ x))\ \lambda x.(\Phi\ (x\ x)) \rightarrow_\beta
   (\Phi\ (\lambda x.(\Phi\ (x\ x)\ \lambda x.(\Phi\ (x\ x))),$$
et
$$ (\Phi\ F) = (\Phi\ (Y\ \Phi)) \rightarrow_\beta
   (\Phi\ (\lambda x.(\Phi\ (x\ x)\ \lambda x.(\Phi\ (x\ x))),$$
ce qui permet de conclure que
$$ F =_\beta (\Phi\ F).$$

```python
Y = Lambda_terme('!f.(!x.(f (x x)) !x.(f (x x)))')
print(Y)
```

```python
FACTv3 = Y.applique(PHI_FACT)
```

```python
FACTv3.applique(ZERO).forme_normale() == UN
```

```python
FACTv3.applique(UN).forme_normale() == UN
```

```python
FACTv3.applique(DEUX).forme_normale(nb_etapes_max=248) == DEUX
```

```python
FACTv3.applique(TROIS).forme_normale(nb_etapes_max=1525) == SIX
```

```python
FACTv3.applique(QUATRE).forme_normale(nb_etapes_max=10384) == int_en_church(24)
```

**Remarque** $Y$ n'est pas normalisable, et quelque soit le $\lambda$-terme $M$,  $(Y\ M)$ ne l'est pas. Pourtant ces derniers termes peuvent s'avérer utiles.  

```python
PF = Y.applique(Lambda_terme('M'))
```

```python
PF.forme_normale(verbose=True, nb_etapes_max=10)
```

#### Un autre combinateur de point fixe


Voici un autre combinateur de point fixe, dû à Turing.

$$\Theta = (\lambda x.\lambda y.(y\ ((x\ x)\ y))\ \lambda x.\lambda y.(y\ ((x\ x)\ y))).$$

```python
THETA = Lambda_terme('(!x.!y.(y ((x x) y)) !x.!y.(y ((x x) y)))')
print(THETA)
```

Ce combinateur est un redex, et c'est le seul redex parmi ses sous-termes.une étape de réduction donne

$$ \Theta \rightarrow_\beta \lambda y.(y\ (\Theta\ y)).$$

Par conséquent, en réduisant le redex le plus à gauche, en deux étapes on obtient
$$ (\Theta\ \Phi) \rightarrow_\beta (\lambda y.(y\ (\Theta\ y))\ \Phi) \rightarrow_\beta
   (\Phi\ (\Theta\ \Phi)).$$
Ce qui établit que $\Theta$ est bien un combinateur de point fixe, mais aussi que contrairement à $Y$
$$ (\Theta\ \Phi) \twoheadrightarrow_\beta (\Phi\ (\Theta\ \Phi)).$$

```python
red_theta, _ = THETA.reduit()
print(red_theta)
```

```python
THETA.applique(Lambda_terme('PHI')).forme_normale(verbose=True, nb_etapes_max=2)
```

Utilisons $\Theta$ pour définir une quatrième version de $\mathtt{FACT}$. 

```python
FACTv4 = THETA.applique(PHI_FACT)
```

```python
FACTv4.applique(ZERO).forme_normale() == UN
```

```python
FACTv4.applique(UN).forme_normale() == UN
```

```python
FACTv4.applique(DEUX).forme_normale(nb_etapes_max=252) == DEUX
```

```python
FACTv4.applique(TROIS).forme_normale(nb_etapes_max=1540) == SIX
```

```python
FACTv4.applique(QUATRE).forme_normale(nb_etapes_max=10448) == int_en_church(24)
```

Au titre d'un autre exemple, envisageons maintenant d'établir un $\lambda$-terme qui permet de calculer la longueur d'une liste.

La longueur d'une liste s'exprime récursivement par

\begin{align}
   \mbox{long(<>)} &= 0\\
   \mbox{long(<x,L>)} &= 1 + \mbox{long(L)}.
\end{align}

Avec une couche d'abstraction supplémentaire nous définissons le terme

$$\Phi_{long} = \lambda f.\lambda l.(((\mathtt{IF}\ (\mathtt{LESTVIDE}\ l))\ \mathtt{ZERO})\ (\mathtt{SUC}\ (f\ (\mathtt{LCDR}\ l)))).$$

```python
M_PHI_LONG = Lambda_terme('!f.!l.(((IF (LESTVIDE l)) ZERO)(SUC (f (LCDR l))))')
print(M_PHI_LONG)
PHI_LONG = M_PHI_LONG.subs('IF', IF).subs('LESTVIDE', LESTVIDE).subs('ZERO', ZERO).subs('SUC', SUC).subs('LCDR', LCDR)
```

Définissions le terme $\mathtt{LONG}$ à l'aide de l'un ou l'autre de nos deux combinateurs de point fixe.

$$ \mathtt{LONG} = (\Theta\ \Phi_{long}).$$

```python
LONG = THETA.applique(PHI_LONG)
```

```python
LONG.applique(LVIDE).forme_normale() == ZERO
```

```python
M1 = Lambda_terme('M1')
M2 = Lambda_terme('M2')
M3 = Lambda_terme('M3')
L = LCONS.applique(M1).applique(LCONS.applique(M2).applique(LCONS.applique(M3).applique(LVIDE)))
LONG.applique(L).forme_normale(nb_etapes_max=135) == TROIS
```

#### Et la boucle `while` ?


Bien ! on voit comment construire un $\lambda$-terme exprimant un algorithme récursif. Mais comment exprimer une itération conditionnelle (boucle `while`) ? 


La réponse tient simplement dans le fait qu'une itération conditionnelle s'exprime généralement en suivant le schéma

~~~python
while p(e):
    e = t(e)
~~~
dans lequel 

* `e` désigne l'état courant des variables, 
* `p(e)` exprime une condition dépendant de l'état courant 
* et `t(e)` est un traitement pouvant modifier l'état courant.

Ce schéma peut être reformulé de manière récursive en écrivant

~~~python
def tq(e):
    if p(e):
        e = t(e)
        return tq(e)
    else:
        return e
~~~


Il suffit donc de considérer le $\lambda$-terme

$$\Phi_{while} = \lambda f.\lambda p.\lambda t.\lambda e.(((\mathtt{IF}\ (p\ e))\ (((f\ p)\ t)\ (t\ e))\ e),$$

puis de définir le terme

$$ \mathtt{WHILE} = (Y\ \Phi_{while}),$$
ou 
$$ \mathtt{WHILE} = (\Theta\ \Phi_{while}).$$

```python
M_PHI_WHILE = Lambda_terme('!f.!p.!t.!e.(((IF (p e)) (((f p) t) (t e))) e)')
PHI_WHILE = M_PHI_WHILE.subs('IF', IF)
WHILE = Y.applique(PHI_WHILE)
```

Pour terminer, utilisons notre terme $\mathtt{WHILE}$ pour construire une terme permettant de calculer la division euclidienne de deux entiers, dernière opération arithmétique de base que nous n'avons pas réalisée.


On veut un terme $\mathtt{DIV}$ qui comme la fonction `divmod` de Python donne, sous forme d'un couple, le quotient et le reste de la division d'un entier $m$ par un entier $n$.

On pourrait programmer cette fonction en Python de cette façon :

~~~python
def divmod(m, n):
    q, r = 0, m
    while r >= n:
        q, r = q + 1, r - n
    return (q, r)
~~~
Dans cet algorithme 
* l'état `e`  est le triplet de variables `(q, r, n)`
* la condition `p(e)` est exprimée par l'inégalité `r >= n`
* et le traitement `t(e)` modifiant l'état courant est le construction du couple `(q + 1, r - n, n)`.

\begin{align}
 P &= \lambda e.((\mathtt{INF}\ (\mathtt{CDR}\ (\mathtt{CDR}\ e))) (\mathtt{CAR}\ (\mathtt{CDR}\ e)))\\
 T &= \lambda e.((\mathtt{CONS}\ (\mathtt{SUC}\ (\mathtt{CAR}\ e))) ((\mathtt{CONS}\ ((\mathtt{SUB}\ (\mathtt{CAR}\ (\mathtt{CDR}\ e))) (\mathtt{CDR}\ (\mathtt{CDR}\ e)))) (\mathtt{CDR}\ (\mathtt{CDR}\ e))))\\
 \mathtt{DIVMOD} &= \lambda m.\lambda n.((((\mathtt{WHILE}\ P))\ T)\ [\lceil 0\rceil, [m, n]]).
\end{align}

```python
M_P = Lambda_terme('!e.((INF (CDR (CDR e))) (CAR (CDR e)))')
print(M_P)
P = M_P.subs('INF', INF).subs('CAR', CAR).subs('CDR', CDR)
M_T = Lambda_terme('!e.((CONS (SUC (CAR e))) ((CONS ((SUB (CAR (CDR e))) (CDR (CDR e)))) (CDR (CDR e))))')
print(M_T)
T = M_T.subs('CONS', CONS).subs('CAR', CAR).subs('CDR', CDR).subs('SUC', SUC).subs('SUB', SUB)
M_DIVMOD = Lambda_terme('!m.!n.(((WHILE P) T) ((CONS ZERO) ((CONS m) n)))')
print(M_DIVMOD)
DIVMOD = M_DIVMOD.subs('WHILE', WHILE).subs('P', P).subs('T', T).subs('CONS', CONS).subs('ZERO', ZERO)
print(DIVMOD)
```

```python
%%time
tests = []
for a in range(10):
    for b in range(1, 10):
        q, r = divmod(a, b)
        A, B = int_en_church(a), int_en_church(b)
        Q, R = int_en_church(q), int_en_church(r)
        res = DIVMOD.applique(A).applique(B).forme_normale(nb_etapes_max=10000)
        #print(res)
        tests.append((a, b, res == CONS.applique(Q).applique(CONS.applique(R).applique(B)).forme_normale()))
all(t[2] for t in tests)
```

## Conclusion


Nous arrêtons là ce premier contact avec le $\lambda$-calcul.

Nous avons vu que ce langage très élémentaire, avec l'abstraction et l'application pour seules constructions, et la règle de $\beta$-réduction pour seule transformation de $\lambda$-termes, permet de représenter les données de base de n'importe quel langage de programmation, les booléens, les entiers, les couples, les listes, et permet d'exprimer les expressions conditionnelles, les itérations conditionnelles ou non, et la récursivité. En fait le $\lambda$-calcul est un langage Turing-complet ... même s'il est particulièrement inefficace.

D'autres sujets relatifs au $\lambda$-calcul n'ont pas été abordés :

* stratégies de réduction : paresseuse, par valeurs ..., et leurs conséquences.
* $\lambda$-calcul typé.

<!-- #region toc-hr-collapsed=true toc-nb-collapsed=true -->
# $\lambda$-calcul avec les lambda-expressions de Python
<!-- #endregion -->

Dans cette partie, les lambda-expressions de Python vont être utilisées pour représenter les abstractions, et les applications seront des appels de fonction.

Les seuls mots du langage Python que nous utiliserons seront `lambda` et `if`. Les autres mots (`def`, `while`, `for` ...) seront bannis. Nous utiliserons aussi les entiers prédéfinis dans le langage avec certaines opérations arithmétiques.

<!-- #region toc-hr-collapsed=true toc-nb-collapsed=true -->
## Les booléens
<!-- #endregion -->

```python
vrai = lambda x: lambda y: x
faux = lambda x: lambda y: y
```

```python
def booleen_en_bool(b):
    return b(True)(False)
```

```python
tuple(booleen_en_bool(b) for b in (vrai, faux))
```

```python
If = lambda c: lambda a: lambda s: c(a)(s) 
```

```python
If(vrai)(1)(2)
```

```python
If(faux)(1)(2)
```

```python
#If(vrai)(1)(1/0)
```

```python
non = lambda b: If(b)(faux)(vrai)
```

```python
tuple(booleen_en_bool(non(b)) for b in (vrai, faux))
```

```python
et = lambda b1: lambda b2: If(b1)(b2)(faux)
```

```python
tuple(booleen_en_bool(et(b1)(b2)) for b1 in (vrai, faux) 
      for b2 in (vrai, faux))
```

```python
ou = lambda b1: lambda b2: If(b1)(vrai)(b2)
```

```python
tuple(booleen_en_bool(ou(b1)(b2)) for b1 in (vrai, faux) 
      for b2 in (vrai, faux))
```

<!-- #region toc-hr-collapsed=true toc-nb-collapsed=true -->
## Les entiers de Church
<!-- #endregion -->

```python
zero = lambda f: lambda x: x
```

```python
un = lambda f: lambda x: f(x)
```

```python
deux = lambda f: lambda x: f(f(x))
```

```python
trois = lambda f: lambda x: f(f(f(x)))
```

```python
def entier_church_en_int(ec):
    return ec(lambda n: n+1)(0)
```

```python
tuple(entier_church_en_int(n) for n in (zero, un, deux, trois))
```

```python
suc = lambda n: lambda f: lambda x: f(n(f)(x))
```

```python
tuple(entier_church_en_int(suc(n)) for n in (zero, un, deux, trois)) 
```

```python
def int_en_entier_church(n):
    if n == 0:
        return zero
    else:
        return suc(int_en_entier_church(n - 1))
```

```python
tuple(entier_church_en_int(int_en_entier_church(n)) for n in range(10))
```

```python
add = lambda n: lambda m: lambda f: lambda x: n(f)(m(f)(x))
```

```python
cinq = add(deux)(trois)
entier_church_en_int(cinq)
```

```python
mul = lambda n: lambda m: lambda f: n(m(f))
```

```python
six = mul(deux)(trois)
entier_church_en_int(six)
```

```python
exp = lambda n: lambda m: m(n)
```

```python
huit = exp(deux)(trois)
entier_church_en_int(huit)
```

```python
neuf = exp(trois)(deux)
entier_church_en_int(neuf)
```

```python
est_nul = lambda n : n(lambda x: faux)(vrai)
```

```python
tuple(booleen_en_bool(est_nul(n)) 
      for n in (zero, un, deux, trois, cinq, six, huit))
```

<!-- #region toc-hr-collapsed=true toc-nb-collapsed=true -->
## Les couples
<!-- #endregion -->

```python
cons = lambda x: lambda y: lambda z: z(x)(y)
```

```python
un_deux = cons(un)(deux)
```

```python
car = lambda c: c(vrai)
cdr = lambda c: c(faux)
```

```python
entier_church_en_int(car(un_deux)), entier_church_en_int(cdr(un_deux))
```

```python
pred = lambda n: car(n(lambda c: cons(cdr(c))(suc(cdr(c))))(cons(zero)(zero)))
```

```python
tuple(entier_church_en_int(pred(int_en_entier_church(n))) for n in range(10))
```

```python
sub = lambda n: lambda m: m(pred)(n)
```

```python
entier_church_en_int(sub(huit)(trois))
```

```python
est_inf_ou_egal = lambda n: lambda m: est_nul(sub(m)(n))
```

```python
tuple(booleen_en_bool(est_inf_ou_egal(cinq)(int_en_entier_church(n))) 
      for n in range(10))
```

```python
est_egal = lambda n: lambda m: et(est_inf_ou_egal(n)(m))(est_inf_ou_egal(m)(n))
```

```python
tuple(booleen_en_bool(est_egal(cinq)(int_en_entier_church(n))) 
      for n in range(10))
```

<!-- #region toc-hr-collapsed=true toc-nb-collapsed=true -->
## Itération
<!-- #endregion -->

```python
fact = lambda n: cdr(n(lambda c: (cons(suc(car(c)))(mul(suc(car(c)))(cdr(c)))))(cons(zero)(un)))
```

```python
tuple(entier_church_en_int(fact(int_en_entier_church(n))) for n in range(7))
```

<!-- #region toc-hr-collapsed=true toc-nb-collapsed=true -->
## Combinateur de point fixe
<!-- #endregion -->

```python
phi_fact = lambda f: lambda n: 1 if n == 0 else n*f(n-1)
```

```python
bottom = lambda x: (lambda y: y(y))(lambda y:y(y))
```

```python
f0 = phi_fact(bottom)
f1 = phi_fact(f0)
f2 = phi_fact(f1)
f3 = phi_fact(f2)
f4 = phi_fact(f3)
```

```python
tuple(f4(n) for n in range(4))
```

```python
def fact_rec(n):
    if n == 0:
        return 1
    else:
        return n * fact_rec(n - 1)
```

```python
fact2 = phi_fact(fact_rec)
```

```python
tuple(fact2(n) for n in range(7))
```

```python
fix_curry = lambda f: (lambda x: lambda y: f(x(x))(y))(lambda x: lambda y: f(x(x))(y))
```

```python
fact3 = fix_curry(phi_fact)
```

```python
tuple(fact3(n) for n in range(7))
```

<!-- #region toc-hr-collapsed=true toc-nb-collapsed=true -->
## Un programme obscur
<!-- #endregion -->

```python
print((lambda x: (lambda y: lambda z: x(y(y))(z))(lambda y: lambda z: x(y(y))(z))) 
      (lambda x: lambda y: '' if y == [] else chr(y[0])+x(y[1:]))
      (((lambda x: (lambda y: lambda z: x(y(y))(z)) (lambda y: lambda z: x(y(y))(z)))
        (lambda x: lambda y: lambda z: [] if z == [] else [y(z[0])]+x(y)(z[1:])))      
       (lambda x: (lambda x: (lambda y: lambda z: x(y(y))(z))(lambda y: lambda z: x(y(y))(z)))
        (lambda x: lambda y: lambda z: lambda t: 1 if t == 0 else (lambda x: ((lambda u: 1 if u == 0 else z)(t % 2)) * x * x % y)
         (x(y)(z)(t // 2)))(989)(x)(761))
       ([377, 900, 27, 27, 182, 647, 163, 182, 390, 27, 726, 937])))
```

```python
phiListEnChaine = lambda x: lambda y: '' if y == [] else chr(y[0]) + x(y[1:])
```

```python
fix_curry(phiListEnChaine)([65+k for k in range(26)])
```

```python
phiMap = lambda x: lambda y: lambda z: [] if z == [] else [y(z[0])] + x(y)(z[1:])
```

```python
fix_curry(phiMap)(lambda x: x*x)([1, 2, 3, 4])
```

```python
phiExpoMod = lambda x: lambda y: lambda z: lambda t: 1 if z == 0 else (lambda u: 1 if u == 0 else y)(z % 2) * x(y)(z//2)(t) ** 2 % t
```

```python
fix_curry(phiExpoMod)(2)(10)(1000)
```

```python

```

66 KiB Raw Blame History Unescape Escape